Question

【题目】如图，过A(8，0)、B(0，8)两点的直线y1与直线y2＝x+2交于点C.直线y2与x轴、y轴分别交于点D和点E.

(1)动点M从A点出发沿AB运动，运动的速度是每秒1个单位长度：当点M运动到B点时停止运动，设M运动时间为t秒，△ADM的面积为S，求S与t的函数关系式.

(2)在y轴上是否存在点P，使△ACP为等腰三角形？若存在，请直接写出点P的坐标；若不存在，请说明理由.

Answer 1

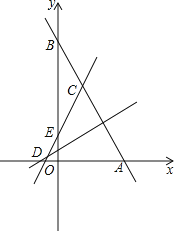
【答案】(1)S＝t(0＜t≤8)；(2)存在，点P的坐标为(0，﹣6)或(0，6)或(0，5﹣)或(0，5+)或(0，).

【解析】

(1)先求出点D坐标，进而得出AD＝10，再判断出△AMH∽△ABO，进而用t表示出MH，最后用三角形面积公式即可得出结论；

(2)利用待定系数法求出直线AB的解析式，进而联立直线CD解析式求出点C坐标，分三种情况，用两边相等建立方程求解即可得出结论.

(1)如图，针对于直线y2＝x+2，

令y＝0，则x+2＝0，

∴x＝﹣3，

∴D(﹣2，0)，

∵A(8，0)，

∴AD＝8﹣(﹣2)＝10，

∵A(8，0)、B(0，8)，

∴AB＝＝16，

由运动知AM＝t，过点M作MH⊥x轴于H，

∴MH∥OB，

∴△AMH∽△ABO，

∴ ，

∴ ，

∴MH＝t，

∴S＝S△ADM＝ADDH＝×10×t＝t(0＜t≤8)；

(2)设直线AB的解析式为y＝kx+b，

将A(8，0)、B(0，8)代入y＝kx+b中，得，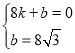

∴ ，

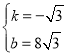∴直线AB的解析式为y＝﹣x+8，

∵直线y2＝x+2交于点C，

联立得， ，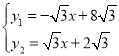

解得， ，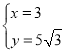

∴C(3，5)，

设P(0，m)，

∵A(8，0)，

∴AC2＝(8﹣3)2+(0﹣5)2＝100，AP2＝64+m2，CP2＝9+(m﹣5)2，

∵△ACP为等腰三角形，

∴①当AC＝AP时，

∴AC2＝AP2，

∴100＝64+m2，

∴m＝±6，

∴P(0，﹣6)或(0，6)，

②当AC＝CP时，

∴AC2＝CP2，

∴100＝9+(m﹣5)2，

∴m＝5±，

∴P(0，5﹣)或(0，5+)

③当AP＝CP时，AP2＝CP2，

∴64+m2＝9+(m﹣5)2，

∴m＝，

∴P(0，)，

即：点P的坐标为(0，﹣6)或(0，6)或(0，5﹣)或(0，5+)或(0，).