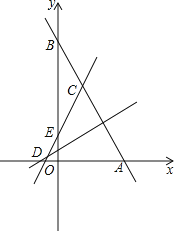ЬтФПФкШн
ЁОЬтФПЁПШчЭМЃЌЕуPЮЊxжсе§АыжсЩЯЕФвЛИіЕуЃЌЙ§ЕуPзїxжсЕФДЙЯпЃЌНЛКЏЪ§![]() ЕФЭМЯѓгкЕуAЃЌНЛКЏЪ§
ЕФЭМЯѓгкЕуAЃЌНЛКЏЪ§![]() ЕФЭМЯѓгкЕуBЃЌЙ§ЕуBзїxжсЕФЦНааЯпЃЌНЛ
ЕФЭМЯѓгкЕуBЃЌЙ§ЕуBзїxжсЕФЦНааЯпЃЌНЛ![]() гкЕуCЃЌБпНгACЃЎ
гкЕуCЃЌБпНгACЃЎ
ЃЈ1ЃЉЕБЕуPЕФзјБъЮЊЃЈ1ЃЌ0ЃЉЪБЃЌЧѓЁїABCЕФУцЛ§ЃЛ
ЃЈ2ЃЉЕБЕуPЕФзјБъЮЊЃЈ1ЃЌ0ЃЉЪБЃЌдкyжсЩЯЪЧЗёДцдквЛЕуQЃЌЪЙAЁЂOЁЂQШ§ЕуЮЊЖЅЕуЕФШ§НЧаЮЁїQAOЮЊЕШбќШ§НЧаЮЃПШєДцдкЃЌЧыжБНгаДГіQЕуЕФзјБъЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ЃЈ3ЃЉЧыФуСЌНгOAКЭOCЃЎЕБЕуPЕФзјБъЮЊЃЈtЃЌ0ЃЉЪБЃЌЁїOACЕФУцЛ§ЪЧЗёЫцtЕФжЕЕФБфЛЏЖјБфЛЏЃПЧыЫЕУїРэгЩЃЎ

ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉдђQЕФзјБъЮЊЃЈ0ЃЌЉ
ЃЛЃЈ2ЃЉдђQЕФзјБъЮЊЃЈ0ЃЌЉ![]() ЃЉЃЌЃЈ0ЃЌ
ЃЉЃЌЃЈ0ЃЌ![]() ЃЉЃЌЃЈ0ЃЌ2ЃЉЛђЃЈ0ЃЌ1ЃЉЃЛ
ЃЉЃЌЃЈ0ЃЌ2ЃЉЛђЃЈ0ЃЌ1ЃЉЃЛ
ЃЈ3ЃЉМћНтЮі.
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнPЕузјБъЯШЧѓГіAЃЌBСНЕузјБъЃЌШЛКѓЧѓГіCЕузјБъЃЌЕУЕНAB=3ЃЌBC=![]() ЃЌдйРћгУШ§НЧаЮУцЛ§ЙЋЪНЧѓНтМДПЩЃЛ
ЃЌдйРћгУШ§НЧаЮУцЛ§ЙЋЪНЧѓНтМДПЩЃЛ
ЃЈ2ЃЉШчЭМЂйЃЌЯШЧѓЕУOA=![]() ЃЌдйЗжOA=OQЃЌAQ=AOЃЌQO=QAШ§жжЧщПіЃЌЗжБ№ЧѓГіQЕузјБъМДПЩЃЛ
ЃЌдйЗжOA=OQЃЌAQ=AOЃЌQO=QAШ§жжЧщПіЃЌЗжБ№ЧѓГіQЕузјБъМДПЩЃЛ
ЃЈ3ЃЉШчЭМЂкЙ§ЕуCзїCEЁЭxжсгкЕуEЃЌCDЁЭyжсгкЕуDЃЌвђЮЊЕуPЕФзјБъЮЊЃЈtЃЌ0ЃЉЃЌЫљвдЕуAЕФзјБъЮЊЃЈtЃЌ![]() ЃЉЃЌЕуBЃЈtЃЌ
ЃЉЃЌЕуBЃЈtЃЌ![]() ЃЉЃЌЕуCЃЈ
ЃЉЃЌЕуCЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌгЩЭМЂкПЩжЊSЁїOAC=SОиаЮCDOE+SЬнаЮAPECЉSЁїOCDЉSЁїOAPЃЌНјЖјПЩЕУЕНЙигкtЕФЗНГЬЃЌШЛКѓНтЗНГЬМДПЩ.
ЃЉЃЌгЩЭМЂкПЩжЊSЁїOAC=SОиаЮCDOE+SЬнаЮAPECЉSЁїOCDЉSЁїOAPЃЌНјЖјПЩЕУЕНЙигкtЕФЗНГЬЃЌШЛКѓНтЗНГЬМДПЩ.
НтЃКЃЈ1ЃЉЕБЕуPЕФзјБъЮЊЃЈ1ЃЌ0ЃЉЪБЃЌЕуAЁЂBЕФКсзјБъЮЊ1ЃЌ
ЁпЕуAдкЗДБШР§КЏЪ§y=![]() ЩЯЃЌЕуBдкЗДБШР§КЏЪ§y=
ЩЯЃЌЕуBдкЗДБШР§КЏЪ§y=![]() ЩЯЃЌ
ЩЯЃЌ
ЁрЕуAЃЈ1ЃЌ1ЃЉЃЌЕуBЃЈ1ЃЌ4ЃЉЃЌ
ЁпBCЁЮxжсЃЌ
ЁрЕуCЕФзнзјБъЮЊ4ЃЌ
гжЁпЕуCдкy=![]() ЩЯЃЌ
ЩЯЃЌ
ЁрЕуCЕФзјБъЮЊЃЈ![]() ЃЌ4ЃЉЃЌ
ЃЌ4ЃЉЃЌ
ЁрAB=3ЃЌBC=![]() ЃЌ
ЃЌ
ЁрSЁїABC=![]() ЁСBCЁСAB=
ЁСBCЁСAB=![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШчЭМЂйЫљЪОЃКOA=![]() =
=![]() ЃЌ
ЃЌ
ЂйШєOA=OQЃЌЕуQЮЛгкQ1ЛђQ2ЮЛжУЃЌДЫЪБQ1ЃЈ0ЃЌЉ![]() ЃЉЃЌQ2ЃЈ0ЃЌ
ЃЉЃЌQ2ЃЈ0ЃЌ![]() ЃЉЃЛ
ЃЉЃЛ
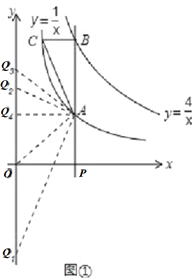
ЂкШєAQ=AOЃЌЕуQЮЛгкQ3ЮЛжУЃЌДЫЪБQ3ЃЈ0ЃЌ2ЃЉЃЛ
ЂлШєQO=QAЃЌЕуQЮЛгкQ4ЮЛжУЃЌДЫЪБQ4ЃЈ0ЃЌ1ЃЉЃЛ
дђQЕФзјБъЮЊЃЈ0ЃЌЉ![]() ЃЉЃЌЃЈ0ЃЌ
ЃЉЃЌЃЈ0ЃЌ![]() ЃЉЃЌЃЈ0ЃЌ2ЃЉЛђЃЈ0ЃЌ1ЃЉЃЛ
ЃЉЃЌЃЈ0ЃЌ2ЃЉЛђЃЈ0ЃЌ1ЃЉЃЛ
ЃЈ3ЃЉЙ§ЕуCзїCEЁЭxжсгкЕуEЃЌCDЁЭyжсгкЕуDЃЌШчЭМЂкЫљЪОЃК
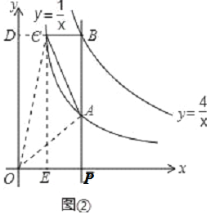
ЁпЕуPЕФзјБъЮЊЃЈtЃЌ0ЃЉЃЌ
ЁрЕуAЕФзјБъЮЊЃЈtЃЌ![]() ЃЉЃЌЕуBЃЈtЃЌ
ЃЉЃЌЕуBЃЈtЃЌ![]() ЃЉЃЌЕуCЃЈ
ЃЉЃЌЕуCЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
ЁрSЁїOAC=SОиаЮCDOE+SЬнаЮAPECЉSЁїOCDЉSЁїOAP=1+![]() ЃЈ
ЃЈ![]() +
+![]() ЃЉЁСЃЈtЉ
ЃЉЁСЃЈtЉ![]() ЃЉЉ
ЃЉЉ![]() Љ
Љ![]() =
=![]() ЃЛ
ЃЛ
ЙЪЁїOACЕФУцЛ§ВЛЫцtЕФжЕЕФБфЛЏЖјБфЛЏЃЎ

 ШЋгХПМЕфЕЅдЊМьВтОэМАЙщРрзмИДЯАЯЕСаД№АИ
ШЋгХПМЕфЕЅдЊМьВтОэМАЙщРрзмИДЯАЯЕСаД№АИ ЦЗбЇЫЋгХОэЯЕСаД№АИ
ЦЗбЇЫЋгХОэЯЕСаД№АИ