题目内容
1.(1)1-$\frac{a-b}{a+2b}$$÷\frac{{a}^{2}-{b}^{2}}{{a}^{2}+4ab+4{b}^{2}}$;(2)$\frac{2y-3z}{2yz}+\frac{2z-3x}{3xz}$+$\frac{9x-4y}{6xy}$;
(3)($\frac{a+1}{a-1}+\frac{1}{{a}^{2}-2a+1}$)$÷\frac{a}{a-1}$;
(4)($\frac{4}{{a}^{2}-2a}-\frac{a}{a-2}$)÷(1+$\frac{2}{a}$).
分析 (1)原式第二项利用除法法则变形,约分后两项通分并利用同分母分式的减法法则计算即可得到结果;
(2)原式通分并利用同分母分式的加减法则计算即可得到结果;
(3)原式括号中两项通分并利用同分母分式的加法法则计算,同时利用除法法则变形,约分即可得到结果;
(4)原式括号中两项通分并利用同分母分式的加减法则计算,同时利用除法法则变形,约分即可得到结果.
解答 解:(1)原式=1-$\frac{a-b}{a+2b}$•$\frac{(a+2b)^{2}}{(a+b)(a-b)}$=1-$\frac{a+2b}{a+b}$=$\frac{a+b-a-2b}{a+b}$=-$\frac{b}{a+b}$;
(2)原式=$\frac{6xy-9xz}{6xyz}$+$\frac{4yz-6xy}{6xyz}$+$\frac{9xz-4yz}{6xyz}$=$\frac{6xy-9xz+4yz-6xy+9xz-4yz}{6xyz}$=0;
(3)原式=$\frac{{a}^{2}-1+1}{(a-1)^{2}}$•$\frac{a-1}{a}$=$\frac{a}{a-1}$;
(4)原式=$\frac{4-{a}^{2}}{a(a-2)}$÷$\frac{a+2}{a}$=-$\frac{(a+2)(a-2)}{a(a-2)}$•$\frac{a}{a+2}$=-1.
点评 此题考查了分式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
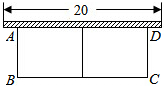 如图,有长为30m的篱笆,一面利用墙(墙的最大可用长度为20m),围成中间隔有一道篱笆(平行于AB)的矩形花圃ABCD.设花圃的一边AB为x(m).
如图,有长为30m的篱笆,一面利用墙(墙的最大可用长度为20m),围成中间隔有一道篱笆(平行于AB)的矩形花圃ABCD.设花圃的一边AB为x(m).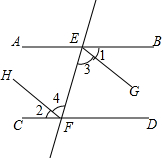 如图,已知∠AEF=∠EFD,∠1=∠2,试证明:EG∥HF.
如图,已知∠AEF=∠EFD,∠1=∠2,试证明:EG∥HF.