题目内容
11.一只蚂蚁从某点M出发,在一条直线上来回爬行,把它向右爬行的路程记为正数,向左爬行的路程记为负数,则它爬过的各段路程依次为:-3cm,+10cm,-8cm,+5cm,-6cm,+12cm,-10cm.(1)问这只蚂蚁最后是否回到了出发点M?
(2)蚂蚁离出发点M最远时是多少厘米?是在出发点的左边还是右边?
(3)蚂蚁在爬行过程中,如果每爬行2cm就1粒芝麻,那么最后它共得到多少粒芝麻?
分析 (1)把记录数据相加,结果为正还是负,说明蚂蚁最后离原点的距离;
(2)分别计算出每次爬行后距离原点的距离;
(3)蚂蚁一共得到的芝麻数,与它爬行的方向无关,只与爬行的距离有关,所以应把绝对值相加,再求得到的芝麻粒数.
解答 解:(1)根据题意可得:向右爬行的路程记为“+”,向左爬行的路程记为“-”.则小蚂蚁最后离开出发点的距离是:
-3+10-8+5-6+12-10=0.
答:小蚂蚁最后回到了出发点M.
(2)-3+10=7,7-8=-1,-1+5=4,4-6=-2,-2+12=10,10-10=0,
小蚂蚁在爬行过程中离出发点M最远时在右边,离开出发点M相距10厘米;
(2)小蚂蚁从离开出发点开始走的路程是:
|-3|+|+10|+|-8|+|+5|+|-6|+|12|+|-10|=54(厘米),
在爬行过程中,小蚂蚁得到的奖励是:
54÷2=27(粒)
答:在爬行过程中,最后它共得到27粒芝麻.
点评 本题主要考查的是有关于正数和负数的题目.解题关键是理解“正”和“负”的相对性,明确什么是一对具有相反意义的量.在一对具有相反意义的量中,先规定其中一个为正,则另一个就用负表示.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
1.A、B、C是平面内的三个点,经过其中任意两点画直线,可以画出的直线有( )
| A. | 1条 | B. | 3条 | C. | 1条或3条 | D. | 无数条 |
2.已知x=$\frac{1}{2}$,y-$\frac{1}{2}$的绝对值为$\frac{3}{2}$,则(5x2y+5xy-7x)-(4x2y+5xy-7x)的值为( )
| A. | -$\frac{1}{4}$或-$\frac{1}{2}$ | B. | $\frac{1}{4}$或-$\frac{1}{2}$ | C. | -$\frac{1}{4}$或$\frac{1}{2}$ | D. | $\frac{1}{4}$或$\frac{1}{2}$ |
6.某工厂某周计划每日生产自行车100辆,由于每日上班人数不一定相等,由于工人实行轮休,实际每日生产量与计划量相比情况如表(增加的为正数,减少的为负数),则本周是增加还是减少?减少,实际生产总量为696辆.
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 七 |
| 增加/辆 | -1 | +3 | -2 | +4 | +7 | -5 | -10 |
3.做一做:竖直转换机,如图所示,两台转换机.
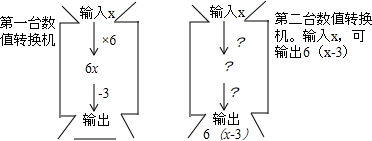
第一台输出的结果是:6x-3 第二台的运算过程为:先-3,再×6.
填写下表:

第一台输出的结果是:6x-3 第二台的运算过程为:先-3,再×6.
填写下表:
| 输入 | -2 | -$\frac{1}{2}$ | 0 | 0.26 | $\frac{1}{3}$ | $\frac{5}{2}$ | 4.5 |
| 第一台的输出 | -15 | -6 | -3 | -1.44 | -2 | 12 | 24 |
| 第二台的输出 | -30 | -9 | -18 | -16.44 | -16 | -3 | 9 |
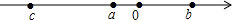 已知a,b,c三个数在数轴上的位置如图所示.
已知a,b,c三个数在数轴上的位置如图所示.