题目内容
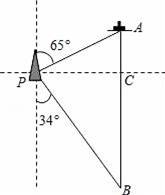
如图,将△ABC绕点P顺时针旋转90°得到△A′B′C′,则点P的坐标是( )


A.(1,1) B.(1,2) C.(1,3) D.(1,4)
B【考点】坐标与图形变化-旋转.
【专题】网格型.
【分析】先根据旋转的性质得到点A的对应点为点A′,点B的对应点为点B′,再根据旋转的性质得到旋转中心在线段AA′的垂直平分线,也在线段BB′的垂直平分线,即两垂直平分线的交点为旋转中心.
【解答】解:∵将△ABC以某点为旋转中心,顺时针旋转90°得到△A′B′C′,
∴点A的对应点为点A′,点C的对应点为点C′,
作线段AA′和CC′的垂直平分线,它们的交点为P(1,2),
∴旋转中心的坐标为(1,2).
故选:B.


【点评】本题考查了坐标与图形变化﹣旋转:图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标.常见的是旋转特殊角度如:30°,45°,60°,90°,180°.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 有意义;
有意义;


 B.
B.
 C.
C.