题目内容
如图,一艘海伦位于灯塔P的北偏东65°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东34°方向上的B处,这时,海伦所在的B处距离灯塔P有多远?(sin65°≈0.91,cos65°≈0.42,sin34°≈0.56,cos34°≈0.83)
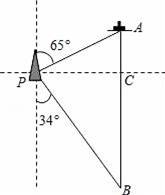

【考点】解直角三角形的应用-方向角问题.
【分析】首先根据题意得出∠APC=90°﹣65°=25°,再利用解直角三角形求出即可.
【解答】解:如图,在Rt△APC中,∠APC=90°﹣65°=25°,
∴PC=PA•cos∠APC≈80×0.91=72.8.
在Rt△BPC中,∠B=34°,
∴PB=
 =
=
 =130(海里),
=130(海里),
答:海轮所在的B处距离灯塔P约有130海里.
【点评】此题主要考查了方向角含义,正确记忆三角函数的定义得出相关角度是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目





 ③y=|x-3④y2=8x.其中y是x的函数的是
③y=|x-3④y2=8x.其中y是x的函数的是
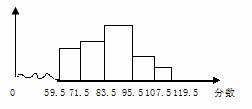 根据(2)中的结论,该区所有参加市模拟考试的学生中,及格人数.优秀人数各约为多少?
根据(2)中的结论,该区所有参加市模拟考试的学生中,及格人数.优秀人数各约为多少?