题目内容
20. 如图,点P是正方形ABCD内的一点,把△ABP绕点B顺时针方向旋转,使点A与点C重合,点P的对应点是Q,若PA=3,PB=2$\sqrt{2}$,PC=5,求∠BQC的度数.
如图,点P是正方形ABCD内的一点,把△ABP绕点B顺时针方向旋转,使点A与点C重合,点P的对应点是Q,若PA=3,PB=2$\sqrt{2}$,PC=5,求∠BQC的度数.
分析 根据题意得出△ABP绕点B顺时针方向旋转了90°,才使点A与C重合,进而得出∠PBQ=90°,再利用勾股定理的逆定理得出∠PQC的度数,进而求出∠BQC的度数.
解答 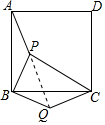 解:如图,连接PQ.
解:如图,连接PQ.
由旋转可知:BQ=BP=2$\sqrt{2}$,QC=PA=3.
又∵ABCD是正方形,
∴△ABP绕点B顺时针方向旋转了90°,才使点A与C重合,
即∠PBQ=90°,
∴∠PQB=45°,PQ=4.
则在△PQC中,PQ=4,QC=3,PC=5,
∴PC2=PQ2+QC2,
即∠PQC=90°.
∴∠BQC=∠PQB+∠PQC=45°+90°=135°.
点评 此题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了勾股定理的逆定理和正方形的性质等知识,利用勾股定理的逆定理得出∠PQC=90°是解题的关键.

练习册系列答案
相关题目
10.下列命题中的假命题是( )
| A. | 同位角一定相等 | B. | 平移不改变图形的形状和大小 | ||
| C. | 无理数是无限不循环小数 | D. | 点M(a,-a)可能在第二象限 |
15.下列说法中正确的是( )
| A. | 直线AB是平角 | B. | 凡是直角都相等 | ||
| C. | 两个锐角的和一定是钝角 | D. | 若AM=$\frac{1}{2}$AB,则点M是线段AB的中点 |
12.下列方程中,不能用直接开平方法解的是( )
| A. | x2-3=0 | B. | x2+2x=0 | C. | (x-1)2-4=0 | D. | (x-1)2=(2x+1)2 |
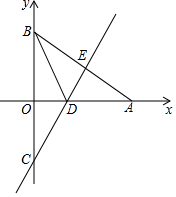 如图,A,B分别在x轴与y轴上,AB=12,∠OAB=30°,将△OAB沿直线ED对折,使点A与点B重合,直线ED分别交y轴、x轴和AB于点C、点D和点E.
如图,A,B分别在x轴与y轴上,AB=12,∠OAB=30°,将△OAB沿直线ED对折,使点A与点B重合,直线ED分别交y轴、x轴和AB于点C、点D和点E.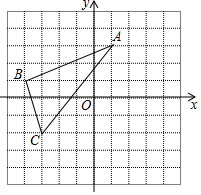 如图,△ABC在平面直角坐标系中,且A(1,3)、B(-4,1)、C(-3,-2).
如图,△ABC在平面直角坐标系中,且A(1,3)、B(-4,1)、C(-3,-2).