题目内容
如图,直线AB分别交y轴、x 轴于A、B两点,OA=2, ,抛物线
,抛物线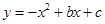 过A、B两点.
过A、B两点.
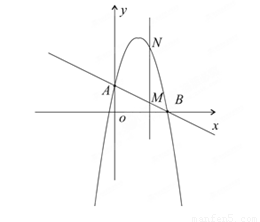
(1)求直线AB和这个抛物线的解析式;
(2)设抛物线的顶点为D,求△ABD的面积
(3)作垂直x轴的直线x=t,在第一象限交直线AB于M,交这个抛物线于N.求当t 取何值时,MN的长度l有最大值?最大值是多少?
【答案】
(1)抛物线的解析式为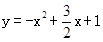 ,直线AB的解析式为:
,直线AB的解析式为: ;
;
(2)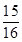 ;(3)当
;(3)当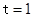 时,
时,
【解析】
试题分析:(1)由已知条件求出A、B的坐标,将其代入即可求出抛物线的解析式和直线AB的解析式.
找出顶点坐标,然后根据 ,即可求出.
,即可求出.
(3) M在直线 :
: 上,N在抛物线
上,N在抛物线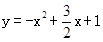 上,可以用t表示出MN的长度,即可找出t为何值时,MN的值最大.
上,可以用t表示出MN的长度,即可找出t为何值时,MN的值最大.
试题解析:
(1)在 中,
中,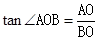
即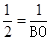
∴BO=2
∴A(0,1),B(2,0)
∵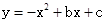 过A(0,1),B(2,0)
过A(0,1),B(2,0)
∴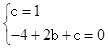
解得: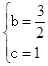
∴抛物线的解析式为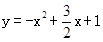
设直线AB解析式为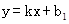 ,将A(0,1),B(2,0)代入
,将A(0,1),B(2,0)代入
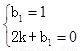 解得:
解得:
∴直线AB的解析式为:
(2)过点D作DE⊥y轴于点E
由(1)抛物线解析式为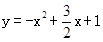
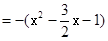
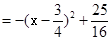
∴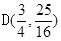
∴ED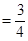 ,EO=
,EO=
∴AE=EO-OA=
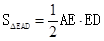


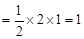
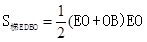
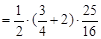
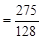

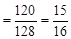
(3)由题可知,M、N横坐标均为t.
∵M在直线 :
: 上
上
∴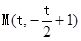
∵N在抛物线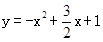 上
上
∴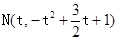
∴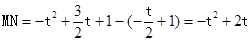
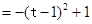 ,其中
,其中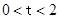 .
.
∴当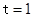 时,
时,
考点:二次函数综合题.

练习册系列答案
相关题目
 轴正半轴).
轴正半轴). 如图.直线AB分别交y轴,x轴于A,B两点,已知A(0,2
如图.直线AB分别交y轴,x轴于A,B两点,已知A(0,2 轴正半轴).
轴正半轴).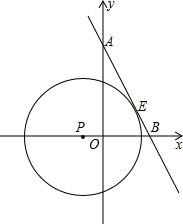 如图.直线AB分别交y轴,x轴于A,B两点,已知A(0,2
如图.直线AB分别交y轴,x轴于A,B两点,已知A(0,2 ),B(2,0),以P(-
),B(2,0),以P(- ,0)为圆心的圆与直线AB相切于点E.
,0)为圆心的圆与直线AB相切于点E.