题目内容
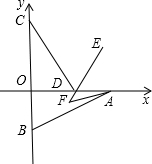
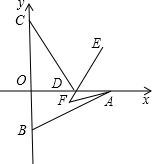
 如图.直线AB分别交y轴,x轴于A,B两点,已知A(0,2
如图.直线AB分别交y轴,x轴于A,B两点,已知A(0,2| 3 |
| 1 |
| 2 |
(1)求⊙P的半径长.
(2)若Rt△ABO被直线y=kx-2k分成两部分,设靠近原点那一部分面积为S,求出S与自变量k的函数关系式.
(3)若直线y=kx-2k把Rt△ABO分成两部分的面积比为1:2,求k的值.
分析:(1)连接PE,由相似三角形的判定定理得出△AOB∽△PEB,再根据相似三角形的对应边成比例即可得出PE的长;
(2))在y=kx-2k中,令y=0,则x=2,故可得出直线y=kx-2k经过点(2,0),设直线y=kx-2k与y轴交于点C,则C(0,-2k),由三角形的面积公式即可得出结论;
(3)当点C是OA的一个三等分点时,根据直线y=kx-2k把Rt△ABO分成两部分的面积比为1:2,可知S△COB:S△ABO=1:2,或S△ABO:S△COB=1:2,
再由三角形的面积公式即可得出结论.
(2))在y=kx-2k中,令y=0,则x=2,故可得出直线y=kx-2k经过点(2,0),设直线y=kx-2k与y轴交于点C,则C(0,-2k),由三角形的面积公式即可得出结论;
(3)当点C是OA的一个三等分点时,根据直线y=kx-2k把Rt△ABO分成两部分的面积比为1:2,可知S△COB:S△ABO=1:2,或S△ABO:S△COB=1:2,
再由三角形的面积公式即可得出结论.
解答: 解:(1)连接PE,
解:(1)连接PE,
∵AB切⊙P于点E,
∴PE⊥AB,
∴∠AOB=∠PEB=90°,
∵∠B=∠B,
∴△AOB∽△PEB,
∴
=
,
∵OA=2
,PB=2+
=2
,AB=
=4,
∴
=
,解得PE=
;
(2)∵在y=kx-2k中,令y=0,则x=2,
∴直线y=kx-2k经过点(2,0),
设直线y=kx-2k与y轴交于点C,则C(0,-2k),
∴S△BOC=
OB•OC=
×2×(-2k)=-2k,此时0<-2k<2
,
∴-
<k<0,
∴S=-2k(-
<k<0);
(3)当点C是OA的一个三等分点时,
∵直线y=kx-2k把Rt△ABO分成两部分的面积比为1:2,
∴S△COB:S△ABO=1:2,或S△ABO:S△COB=1:2,
当S△COB:S△ABC=1:2时,
S△COB=
S△ABO=
×
×2×2
=
,
∴-2k=
,解得k=-
;
当S△ABO:S△COB=1:2时,S△COB=
S△AOB=
×
×2×2
=
,
∴-2k=
,解得k=-
,
综上所述,k=-
或k=-
.
 解:(1)连接PE,
解:(1)连接PE,∵AB切⊙P于点E,
∴PE⊥AB,
∴∠AOB=∠PEB=90°,
∵∠B=∠B,
∴△AOB∽△PEB,
∴
| PE |
| OA |
| PB |
| AB |
∵OA=2
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
22+(2
|
∴
| PE | ||
2
|
2
| ||
| 4 |
5
| ||
| 4 |
(2)∵在y=kx-2k中,令y=0,则x=2,
∴直线y=kx-2k经过点(2,0),
设直线y=kx-2k与y轴交于点C,则C(0,-2k),
∴S△BOC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
∴-
| 3 |
∴S=-2k(-
| 3 |
(3)当点C是OA的一个三等分点时,
∵直线y=kx-2k把Rt△ABO分成两部分的面积比为1:2,
∴S△COB:S△ABO=1:2,或S△ABO:S△COB=1:2,
当S△COB:S△ABC=1:2时,
S△COB=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 3 |
∴-2k=
2
| ||
| 3 |
| ||
| 3 |
当S△ABO:S△COB=1:2时,S△COB=
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 3 |
∴-2k=
| 4 |
| 3 |
| 3 |
2
| ||
| 3 |
综上所述,k=-
| ||
| 3 |
2
| ||
| 3 |
点评:本题考查的是圆的综合题,涉及到切线的性质、相似三角形的判定与性质、三角形的面积公式等知识,难度适中.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 轴正半轴).
轴正半轴). ,抛物线
,抛物线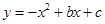 过A、B两点.
过A、B两点.
 轴正半轴).
轴正半轴).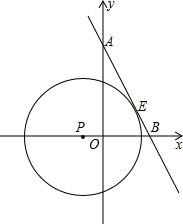 如图.直线AB分别交y轴,x轴于A,B两点,已知A(0,2
如图.直线AB分别交y轴,x轴于A,B两点,已知A(0,2 ),B(2,0),以P(-
),B(2,0),以P(- ,0)为圆心的圆与直线AB相切于点E.
,0)为圆心的圆与直线AB相切于点E.