题目内容
 如图,△ABC的两个外角平分线交于D点,若∠D=65゜,则∠B等于
如图,△ABC的两个外角平分线交于D点,若∠D=65゜,则∠B等于
- A.60゜
- B.70゜
- C.50゜
- D.40゜
C
分析:先根据三角形外角的性质得出∠EAC=∠B+∠ACB,∠ACF=∠B+∠BAC,再根据角平分线的性质得出∠DAC= ∠∠EAC=
∠∠EAC= (∠B+∠ACB),∠ACD=
(∠B+∠ACB),∠ACD= ∠ACF=
∠ACF= (∠B+∠BAC),再根据三角形内角和定理即可得出结论.
(∠B+∠BAC),再根据三角形内角和定理即可得出结论.
解答:∵∠EAC与∠ACF是△ABC的外角,
∴∠EAC=∠B+∠ACB,∠ACF=∠B+∠BAC,
∵△ABC的两个外角平分线交于D点,
∴∠DAC= ∠EAC=
∠EAC= (∠B+∠ACB),∠ACD=
(∠B+∠ACB),∠ACD= ∠ACF=
∠ACF= (∠B+∠BAC)②,
(∠B+∠BAC)②,
∵∠DAC+∠ACD+∠D=180°,∠B+∠ACB+∠BAC=180°,
∴ (∠B+∠ACB)+
(∠B+∠ACB)+ (∠B+∠BAC)+∠D=180°,
(∠B+∠BAC)+∠D=180°,
∴ [∠B+(∠B+∠ACB+∠BAC)]+65°=180°,即
[∠B+(∠B+∠ACB+∠BAC)]+65°=180°,即 ∠B+90°=115°,解得∠B=50°.
∠B+90°=115°,解得∠B=50°.
故选C.
点评:本题考查的是三角形内角和定理及三角形外角的性质,熟知三角形的内角和等于180°是解答此题的关键.
分析:先根据三角形外角的性质得出∠EAC=∠B+∠ACB,∠ACF=∠B+∠BAC,再根据角平分线的性质得出∠DAC=
 ∠∠EAC=
∠∠EAC= (∠B+∠ACB),∠ACD=
(∠B+∠ACB),∠ACD= ∠ACF=
∠ACF= (∠B+∠BAC),再根据三角形内角和定理即可得出结论.
(∠B+∠BAC),再根据三角形内角和定理即可得出结论.解答:∵∠EAC与∠ACF是△ABC的外角,
∴∠EAC=∠B+∠ACB,∠ACF=∠B+∠BAC,
∵△ABC的两个外角平分线交于D点,
∴∠DAC=
 ∠EAC=
∠EAC= (∠B+∠ACB),∠ACD=
(∠B+∠ACB),∠ACD= ∠ACF=
∠ACF= (∠B+∠BAC)②,
(∠B+∠BAC)②,∵∠DAC+∠ACD+∠D=180°,∠B+∠ACB+∠BAC=180°,
∴
 (∠B+∠ACB)+
(∠B+∠ACB)+ (∠B+∠BAC)+∠D=180°,
(∠B+∠BAC)+∠D=180°,∴
 [∠B+(∠B+∠ACB+∠BAC)]+65°=180°,即
[∠B+(∠B+∠ACB+∠BAC)]+65°=180°,即 ∠B+90°=115°,解得∠B=50°.
∠B+90°=115°,解得∠B=50°.故选C.
点评:本题考查的是三角形内角和定理及三角形外角的性质,熟知三角形的内角和等于180°是解答此题的关键.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
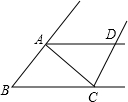 如图,△ABC的两个外角的平分线相交于D,若∠B=50°,则∠ADC=( )
如图,△ABC的两个外角的平分线相交于D,若∠B=50°,则∠ADC=( )| A、60° | B、80° | C、65° | D、40° |
 5、如图:△ABC的两个外角平分线交于点P,则下列结论正确的是( )
5、如图:△ABC的两个外角平分线交于点P,则下列结论正确的是( ) 物线y=a(x+5)2+k过A、B、C三点.
物线y=a(x+5)2+k过A、B、C三点. 如图,△ABC的两个外角平分线交于D点,若∠D=65゜,则∠B等于( )
如图,△ABC的两个外角平分线交于D点,若∠D=65゜,则∠B等于( )