题目内容
 如图,在周长为20的平行四边形ABCD中,AB<AD,AC与BD交于点O,OE⊥BD,交AD于点E,则△ABE的周长为 .
如图,在周长为20的平行四边形ABCD中,AB<AD,AC与BD交于点O,OE⊥BD,交AD于点E,则△ABE的周长为 .
【答案】分析:根据平行四边形的性质求出AB+AD=10,根据线段的垂直平分线求出DE=BE,求出△ABE的周长等于AB+AD,代入求出即可.
解答:解:∵平行四边形ABCD,
∴AD=BC,AB=CD,OB=OD,
∵OE⊥BD,
∴BE=DE,
∵平行四边形ABCD的周长是20,
∴2AB+2AD=20,
∴AB+AD=10,
∴△ABE的周长是AB+AE+BE=AB+AE+DE=AB+AD=10,
故答案为10.
点评:本题考查了线段垂直平分线性质和平行四边形的性质的应用,关键是求出AD+AB的长和求出△ABE的周长=AB+AD,题目具有一定的代表性,难度也不大,是一道比较好的题目.
解答:解:∵平行四边形ABCD,
∴AD=BC,AB=CD,OB=OD,
∵OE⊥BD,
∴BE=DE,
∵平行四边形ABCD的周长是20,
∴2AB+2AD=20,
∴AB+AD=10,
∴△ABE的周长是AB+AE+BE=AB+AE+DE=AB+AD=10,
故答案为10.
点评:本题考查了线段垂直平分线性质和平行四边形的性质的应用,关键是求出AD+AB的长和求出△ABE的周长=AB+AD,题目具有一定的代表性,难度也不大,是一道比较好的题目.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
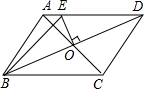 (2012•乌鲁木齐)如图,在周长为20的平行四边形ABCD中,AB<AD,AC与BD交于点O,OE⊥BD,交AD于点E,则△ABE的周长为
(2012•乌鲁木齐)如图,在周长为20的平行四边形ABCD中,AB<AD,AC与BD交于点O,OE⊥BD,交AD于点E,则△ABE的周长为

 如图,在周长为20的平行四边形ABCD中,AB<AD,AC与BD交于点O,OE⊥BD,交AD于点E,则△ABE的周长为________.
如图,在周长为20的平行四边形ABCD中,AB<AD,AC与BD交于点O,OE⊥BD,交AD于点E,则△ABE的周长为________.