题目内容
如图,在周长为20的□ABCD中,AB≠AD,AC、BD相交于点O,点E为边AD上的一点,且BE=DE,则△ABE的周长为

[ ]
A.
4
B.
6
C.
8
D.
10
答案:D
解析:
解析:
|
分析:△ABE的周长=AB+AE+BE.要求△ABE的周长,通常有两种方法:1.分别求出AB、AE、BE的长后相加即可;2.把AB+AE+BE看成一个整体,求其值.就本题而言,应选择第二种方法. 解:在□ABCD中, 因为BE=DE,所以AE+BE=AE+DE=AD. 所以AB+AE+BE=AB+AD. 因为□ABCD的周长为20,且AB=DC,AD=BC, 所以2(AB+AD)=20,即AB+AD=10. 所以AB+AE+BE=10. 故应选D. |

练习册系列答案
相关题目
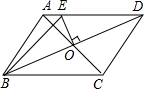 (2012•乌鲁木齐)如图,在周长为20的平行四边形ABCD中,AB<AD,AC与BD交于点O,OE⊥BD,交AD于点E,则△ABE的周长为
(2012•乌鲁木齐)如图,在周长为20的平行四边形ABCD中,AB<AD,AC与BD交于点O,OE⊥BD,交AD于点E,则△ABE的周长为
 如图,在周长为20的平行四边形ABCD中,AB<AD,AC与BD交于点O,OE⊥BD,交AD于点E,则△ABE的周长为________.
如图,在周长为20的平行四边形ABCD中,AB<AD,AC与BD交于点O,OE⊥BD,交AD于点E,则△ABE的周长为________. 如图,在周长为20的平行四边形ABCD中,AB<AD,AC与BD交于点O,OE⊥BD,交AD于点E,则△ABE的周长为 .
如图,在周长为20的平行四边形ABCD中,AB<AD,AC与BD交于点O,OE⊥BD,交AD于点E,则△ABE的周长为 .