题目内容
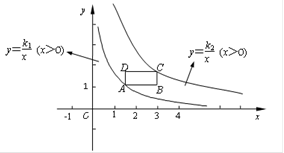
如图,在平面直角坐标系的第一象限中,有一各边所在直线均平行于坐标轴的矩形ABCD,且点A在反比例函数L1:y= (x>0) 的图象上,点C在反比例函数L2:y=
(x>0) 的图象上,点C在反比例函数L2:y=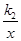 (x>0) 的图象上(矩形ABCD夹在L1与L2之间).(1)若点A坐标为(1,1)时,则L1的解析式为 .(2)在(1)的条件下,若矩形ABCD是边长为1的正方形,求L2的解析式.(3)若k1=1,k2=6,且矩形ABCD的相邻两边分别为1和2,求符合条件的顶点C的坐标.
(x>0) 的图象上(矩形ABCD夹在L1与L2之间).(1)若点A坐标为(1,1)时,则L1的解析式为 .(2)在(1)的条件下,若矩形ABCD是边长为1的正方形,求L2的解析式.(3)若k1=1,k2=6,且矩形ABCD的相邻两边分别为1和2,求符合条件的顶点C的坐标.
 (x>0) 的图象上,点C在反比例函数L2:y=
(x>0) 的图象上,点C在反比例函数L2:y=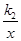 (x>0) 的图象上(矩形ABCD夹在L1与L2之间).(1)若点A坐标为(1,1)时,则L1的解析式为 .(2)在(1)的条件下,若矩形ABCD是边长为1的正方形,求L2的解析式.(3)若k1=1,k2=6,且矩形ABCD的相邻两边分别为1和2,求符合条件的顶点C的坐标.
(x>0) 的图象上(矩形ABCD夹在L1与L2之间).(1)若点A坐标为(1,1)时,则L1的解析式为 .(2)在(1)的条件下,若矩形ABCD是边长为1的正方形,求L2的解析式.(3)若k1=1,k2=6,且矩形ABCD的相邻两边分别为1和2,求符合条件的顶点C的坐标.
(1)y=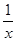 (x>0);(2)y=
(x>0);(2)y= 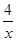 (x>0);符合题意的点C的坐标为(4,
(x>0);符合题意的点C的坐标为(4,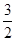 )或(3,2)或(
)或(3,2)或(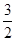 ,4)或(2,3).
,4)或(2,3).
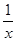 (x>0);(2)y=
(x>0);(2)y= 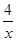 (x>0);符合题意的点C的坐标为(4,
(x>0);符合题意的点C的坐标为(4,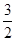 )或(3,2)或(
)或(3,2)或(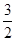 ,4)或(2,3).
,4)或(2,3).试题分析:(1)点A(1,1)在反比例函数y=
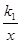 上,则将x=1,y=1代入反比例函数式中,等式一定成立,所以有k1=1.(2)根据题意,将点A向右平移1个单位,再向上平移1个单位,就得到点C,所以点C的坐标是(2,2),将点C(2,2)代入反比例函数y=
上,则将x=1,y=1代入反比例函数式中,等式一定成立,所以有k1=1.(2)根据题意,将点A向右平移1个单位,再向上平移1个单位,就得到点C,所以点C的坐标是(2,2),将点C(2,2)代入反比例函数y=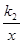 得k2=4.(3)设点A的横坐标是a,则纵坐标是
得k2=4.(3)设点A的横坐标是a,则纵坐标是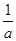 ,分两种情况讨论:当AB=1,AD=2时,此时,点C的坐标应为(a+1,
,分两种情况讨论:当AB=1,AD=2时,此时,点C的坐标应为(a+1, 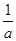 +2),代入直线L2的关系式中,即可求得点C的坐标;当AB=2,AD=1时,点C的坐标可表示为(a+2,
+2),代入直线L2的关系式中,即可求得点C的坐标;当AB=2,AD=1时,点C的坐标可表示为(a+2, 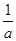 +1),代入直线L2的表达式中,就可求得点C的坐标.
+1),代入直线L2的表达式中,就可求得点C的坐标.试题解析:(1)y=
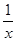 (x>0);(2)y=
(x>0);(2)y=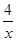 (x>0)
(x>0)(3)①当AB=1,AD=2时,设A点坐标为(a,
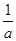 ),则C点坐标为(a+1,
),则C点坐标为(a+1, 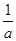 +2),
+2),由已知有(a+1)(
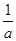 +2)=6,解得a=1或a=
+2)=6,解得a=1或a=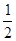
故此时符合条件的C点有(
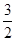 ,4)和(2,3)
,4)和(2,3)②当AB=2,AD=1时,设A点坐标为(a,
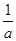 ),则C点坐标为(a+2,
),则C点坐标为(a+2,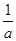 +1),
+1),由已知有(a+2)(
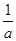 +1)=6,解得a=1或a=2
+1)=6,解得a=1或a=2故此时符合条件的C点有(4,
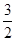 )和(3,2)
)和(3,2)综上所述,符合题意的点C的坐标为(4,
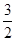 )或(3,2)或(
)或(3,2)或(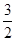 ,4)或(2,3).
,4)或(2,3).
练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
 的图象与反比例函数
的图象与反比例函数 图象的两个交点.
图象的两个交点.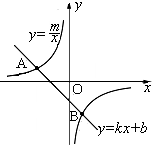
 上,第二象限的点B在反比例函数
上,第二象限的点B在反比例函数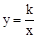 上,且OA⊥OB,
上,且OA⊥OB,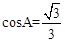 ,则k的值为 ( )
,则k的值为 ( )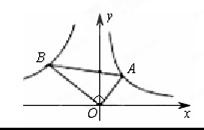
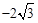
 2,
2,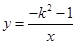 的图象上.下列结论中正确的是( )
的图象上.下列结论中正确的是( )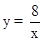 (x>0)的图象分别交于点B1,B2,B3,分别过点B1,B2,B3作x轴的平行线,分别于y轴交于点C1,C2,C3,连接OB1,OB2,OB3,那么图中阴影部分的面积之和为 .
(x>0)的图象分别交于点B1,B2,B3,分别过点B1,B2,B3作x轴的平行线,分别于y轴交于点C1,C2,C3,连接OB1,OB2,OB3,那么图中阴影部分的面积之和为 .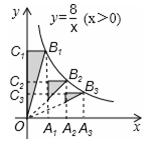
 的图象上,则k的值是( )
的图象上,则k的值是( )



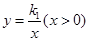 和
和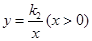 的图象于点P和Q,连接OP和OQ.则下列结论正确的是( )
的图象于点P和Q,连接OP和OQ.则下列结论正确的是( )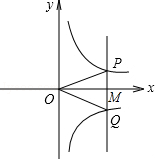
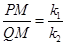
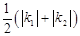
 是反比例函数
是反比例函数 (
( 的图象上的三点,且
的图象上的三点,且 ,则
,则 的大小关系是 ( )
的大小关系是 ( ) 


