题目内容
已知在半径为2cm的圆中,弦AB所对的劣弧长为圆周长的
,则弦AB的长为
| 1 |
| 3 |
2
| 3 |
2
.| 3 |
分析:连接OA、OB,过O作OD⊥AB于D,求出∠AOB,求出∠DOB,求出∠DBO,求出OB,根据勾股定理求出BD,根据垂径定理得出AB=2BD,代入求出即可.
解答: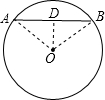 解:连接OA、OB,过O作OD⊥AB于D,
解:连接OA、OB,过O作OD⊥AB于D,
∵弦AB所对的劣弧长为圆周长的
,
∴∠AOB=360°×
=120°,
∵OA=OB,OD⊥AB,
∴∠BOD=
∠AOB=60°,
∵∠ODB=90°,
∴∠DBO=30°,
∴OD=
OB=
×2=1,
由勾股定理得:BD=
=
,
由垂径定理得:AB=2BD=2
,
故答案为:2
.
 解:连接OA、OB,过O作OD⊥AB于D,
解:连接OA、OB,过O作OD⊥AB于D,∵弦AB所对的劣弧长为圆周长的
| 1 |
| 3 |
∴∠AOB=360°×
| 1 |
| 3 |
∵OA=OB,OD⊥AB,
∴∠BOD=
| 1 |
| 2 |
∵∠ODB=90°,
∴∠DBO=30°,
∴OD=
| 1 |
| 2 |
| 1 |
| 2 |
由勾股定理得:BD=
| 22-12 |
| 3 |
由垂径定理得:AB=2BD=2
| 3 |
故答案为:2
| 3 |
点评:本题考查了圆心角、弧、弦之间的关系,垂径定理,勾股定理的应用,主要考查学生应用定理进行推理和计算的能力.

练习册系列答案
相关题目
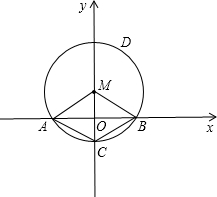 如图,已知⊙M的半径为2cm,圆心角∠AMB=120°,并建立如图所示的直角坐标系.
如图,已知⊙M的半径为2cm,圆心角∠AMB=120°,并建立如图所示的直角坐标系. 如图,在⊙M中,弦AB所对的圆心角∠AMB=120°.已知圆的半径为2cm,并建立如图所示的直角坐标系.
如图,在⊙M中,弦AB所对的圆心角∠AMB=120°.已知圆的半径为2cm,并建立如图所示的直角坐标系. ,则弦AB的长为________.
,则弦AB的长为________.