题目内容
解方程:
①x2-5x=6;
②(x+3)2=(1-2x)2.
①x2-5x=6;
②(x+3)2=(1-2x)2.
考点:解一元二次方程-因式分解法
专题:计算题
分析:①先把方程整理为x2-5x-6=0,然后利用因式分解法解方程;
②先移项得到(x+3)2-(1-2x)2=0,然后利用因式分解法解方程.
②先移项得到(x+3)2-(1-2x)2=0,然后利用因式分解法解方程.
解答:解:①x2-5x-6=0,
(x+1)(x-6)=0,
x+1=0或x-6=0,
所以x1=-1,x2=6;
②(x+3)2-(1-2x)2=0,
(x+3+1-2x)(x+3-1+2x)=0
x+3+1-2x=0或x+3-1+2x=0,
所以x1=4,x2=-
.
(x+1)(x-6)=0,
x+1=0或x-6=0,
所以x1=-1,x2=6;
②(x+3)2-(1-2x)2=0,
(x+3+1-2x)(x+3-1+2x)=0
x+3+1-2x=0或x+3-1+2x=0,
所以x1=4,x2=-
| 2 |
| 3 |
点评:本题考查了解一元二次方程-因式分解法:先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).

练习册系列答案
相关题目

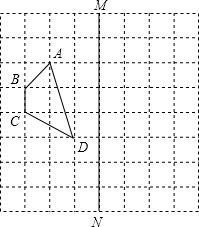 如图,在正方形网络上有一个四边形ABCD.
如图,在正方形网络上有一个四边形ABCD. 如图,O是直线AB上一点,∠BOC=3∠AOC,OC是∠AOD的平分线.
如图,O是直线AB上一点,∠BOC=3∠AOC,OC是∠AOD的平分线.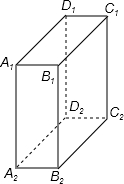 如图,有一个长宽高分别为2cm,1cm,3cm的长方体,有一只小蚂蚁想从点A2爬到点C1处,则它爬行的最短路程为
如图,有一个长宽高分别为2cm,1cm,3cm的长方体,有一只小蚂蚁想从点A2爬到点C1处,则它爬行的最短路程为