题目内容
试说明a、b为何值时，多项式a2+b2-4a+2b+5的值是正数．
考点：配方法的应用,非负数的性质：偶次方
专题：计算题,配方法
分析：先利用配方法得到a2+b2-4a+2b+5=（a-2）2+（b+1）2，然后根据非负数的性质得当a-2≠0且b+1≠0时，a2+b2-4a+2b+5＞0．
解答：解：a2+b2-4a+2b+5=a2-4a+4+b2+2b+1
=（a-2）2+（b+1）2，
∵（a-2）2≥0，（b+1）2≥0，
∴当a-2≠0且b+1≠0时，a2+b2-4a+2b+5＞0，
∴a≠2且b≠-1时，多项式a2+b2-4a+2b+5的值是正数．
=（a-2）2+（b+1）2，
∵（a-2）2≥0，（b+1）2≥0，
∴当a-2≠0且b+1≠0时，a2+b2-4a+2b+5＞0，
∴a≠2且b≠-1时，多项式a2+b2-4a+2b+5的值是正数．
点评：本题考查了配方法：配方法的理论依据是公式a2±2ab+b2=（a±b）2．也考查了非负数的性质．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，x轴、y轴上分别有两点A（3，0）、B（0，2），以点A为圆心，AB为半径的弧交x轴负半轴于点C，则点C的坐标为（ ）| A、（-1，0） | ||||
B、（2-
| ||||
C、（1-
| ||||
D、（3-
|
如图的小正方形边长表示1km，点A相对点B的位置表述正确的是（ ）| A、北偏西45°方向 | ||
| B、南偏东45°方向 | ||
C、北偏西45°方向2
| ||
D、南偏东45°方向2
|
物体如图，则这两个物体的俯视图应是（ ）A、 |
B、 |
C、 |
D、 |
如图，矩形ABCD中，AE⊥BD于E，∠ABD=2∠CBD，BE=2，求AC的长．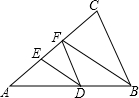
如图，DF∥BC，BF、DE分别平分∠ABC、∠ADF．DE与BF平行吗？为什么？