题目内容
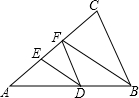 如图,DF∥BC,BF、DE分别平分∠ABC、∠ADF.DE与BF平行吗?为什么?
如图,DF∥BC,BF、DE分别平分∠ABC、∠ADF.DE与BF平行吗?为什么?考点:平行线的判定与性质
专题:证明题
分析:DE∥BF,理由为:由DF与BC平行,利用两直线平行同位角相等得到∠ABC=∠ADF,再由BF、DE分别平分∠ABC、∠ADF,利用角平分线定义得到一对同位角相等,利用同位角相等两直线平行即可得证.
解答:答:DE∥BF,理由为:
证明:∵DF∥BC,
∴∠ADF=∠ABC,
∵BF、DE分别平分∠ABC、∠ADF,
∴∠CBF=∠ABF=
∠ABC,∠FDE=∠ADE=
∠ADF,
∴∠ADE=∠ABF,
∴DE∥BF.
证明:∵DF∥BC,
∴∠ADF=∠ABC,
∵BF、DE分别平分∠ABC、∠ADF,
∴∠CBF=∠ABF=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠ADE=∠ABF,
∴DE∥BF.
点评:此题考查了平行线的判定与性质,熟练掌握平行线的判定与性质是解本题的关键.

练习册系列答案
相关题目
某开发公司今年一月份收益达50万元,且一月份、二月份、三月份的收益共为175万元,问二、三月平均每月的增长率是多少?设平均每月的增长率为x,根据题意可列方程( )
| A、50(1+x)2=175 |
| B、50+50(1+x)2=175 |
| C、50(1+x)+50(1+x)2=175 |
| D、50+50(1+x)+50(1+x)2=175 |
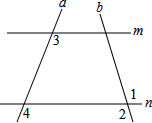 如图,直线a,b,被直线m,n所截,且∠1=∠2,求证:∠3=∠4(填空).
如图,直线a,b,被直线m,n所截,且∠1=∠2,求证:∠3=∠4(填空). 如图,AB为一直线,OD是∠AOC的平分线,OE在∠BOC内,且∠BOE=
如图,AB为一直线,OD是∠AOC的平分线,OE在∠BOC内,且∠BOE=