题目内容
8．
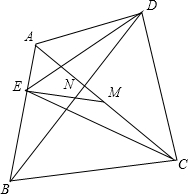如图，凸四边形ABCD中，M、N分别是对角线AC、BD的中点，MN交AB于E．求证：S△CDE=$\frac{1}{2}$SABCD．
分析 连接DM，BM，由M、N分别是对角线AC、BD的中点，又根据等底同高的三角形的面积相等，得到S△CDM=S△ADM，S△DEN=S△BEN，S△ECM=S△AEM，S△MDN=S△BMN，然后根据等式的性质得到即可得到结论．
解答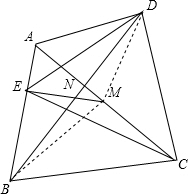 
解：连接DM，BM，
∵M、N分别是对角线AC、BD的中点，
∴S△CDM=S△ADM，S△DEN=S△BEN，S△ECM=S△AEM，S△MDN=S△BMN，
∴S△CDM+S△DEN+S△ECM+S△MDN=S△ADM+S△BEN+S△AEM+S△BMN，
∴S△DEC=S△ADM+S△ABM=$\frac{1}{2}$S△ACD+$\frac{1}{2}$S△ABC=$\frac{1}{2}$S四边形ABCD．
点评 本题考查了等底同高的三角形的面积相等，等式的性质，知道等底等高的两三角形面积相等是解题的关键．
练习册系列答案
相关题目
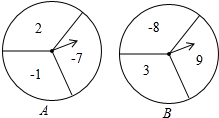如图，两个可以自由转动的均匀转盘，A、B都被平均分成了3份，并在每份内标有一个有理数．有如下游戏规则：
如图，以点P为顶点，射线AB为一边，利用尺规作∠QPB，∠QPB=∠CAB．并说明PQ与AC的位置关系．
如图所示，某海军基地位于A处，在其正南方向100海里处有一重要目标B，在B的正东方向100海里处也有一重要目标C，小岛D位于AC的中点，岛上有一补给码头，一艘军舰从A出发，经B到C匀速航行，一艘补给船同时从D出发，沿南偏西方向匀速直线航行，欲将一批物品送达军舰，已知军舰的速度是补给船的2倍，军舰在由B到C的途中与补给船相遇，那么相遇时补给船航行了多少海里（结果精确到0.1海里）？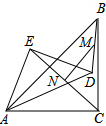
已知等腰Rt△ABC和等腰Rt△ABC中，∠ACB=∠AED=90°，且AD=AC，若点M、N分别是DB、EC的中点，证明：MN⊥EC，MN=$\frac{1}{2}$EC．