Question

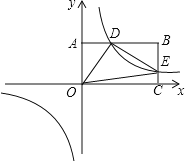
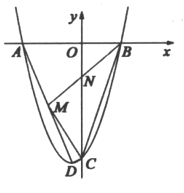
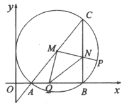
【题目】如图，在平面直角坐标系中，与y轴相切的与x轴交于A、B两点，AC为直径，，，连结BC，点P为劣弧上点，点Q为线段AB上点，且，与交于点，则当 NQ平分时，点P坐标是________.

Answer 1

【答案】(，)

【解析】

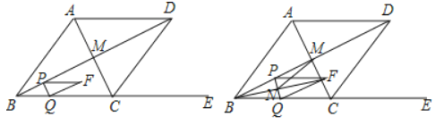
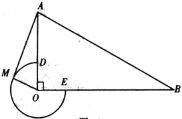
作MK⊥AB，ME⊥BC，PF⊥MK，求证出，，再证明△QMN△QBN，证明出并设MN=BN=x，则EN=4-x，求出x，再证明出△EMN△PMF，

利用相似求出FK=MK-MF=4-=，OK+PF=5+=,即可求出坐标．

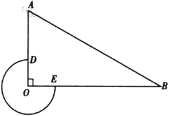
如图：作MK⊥AB，ME⊥BC，PF⊥MK，

∵ME⊥BC，AB⊥BC，，

∴ ,

∴ ,

又直径，，，

∴BC=8，

同理：，

∵，

∴∠QMN=∠NBQ=90°，

∵NQ平分，

∴QM=QB，

∴△QMN△QBN，

∴MN=BN，

∵ME⊥BC，

∴,

设MN=BN=x，则EN=4-x，

∵ ，

∴，

解得x=，

∴MN=BN=，则EN=，

又PF⊥MK，ME⊥BC，

∴△EMN△PMF，

∴，

∵MP=5，

∴ ，

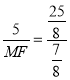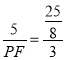
解得MF=，PF=，

∴FK=MK-MF=4-=，OK+PF=5+=,

即P点纵坐标为，横坐标为，

即P点坐标为(，)．

故答案为：(，)．