题目内容
6.若关于x的方程-2x+m$\sqrt{2017-x}$+4020=0存在整数解,则正整数m的所有取值的和为15.分析 由题意m=$\frac{2x-4020}{\sqrt{2017-x}}$,令y=$\sqrt{2017-x}$,则x=2017-y2,可得m=$\frac{2(2017-{y}^{2})-4020}{y}$=$\frac{14}{y}-2y$,由m是正整数,y≥0,推出y=1时,m=12,y=2时,m=3,由此即可解决问题.
解答 解:由题意m=$\frac{2x-4020}{\sqrt{2017-x}}$,令y=$\sqrt{2017-x}$,则x=2017-y2,
∴m=$\frac{2(2017-{y}^{2})-4020}{y}$=$\frac{14}{y}-2y$,
∵m是正整数,y≥0,
∴y=1时,m=12,
y=2时,m=3,
∴正整数m的所有取值的和为15,
故答案为15.
点评 本题考查无理方程、换元法、正整数等知识,解题的关键是学会利用换元法解决问题,属于中考填空题中的压轴题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.下列运算正确的是( )
| A. | 5x2•x3=5x5 | B. | 2x+3y=5xy | C. | 4x8÷2x2=4x4 | D. | (-x3)2=x5 |
18.-3的绝对值是( )
| A. | -3 | B. | 3 | C. | ±3 | D. | $\frac{1}{3}$ |
15.肥皂泡的泡壁厚度大约是0.00000071米,数字0.00000071用科学记数法表示为( )
| A. | 7.1×107 | B. | 0.71×10-6 | C. | 7.1×10-7 | D. | 71×10-8 |
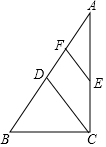 如图,在Rt△ABC中,∠ACB=90°,点D,E分别是AB,AC的中点,点F是AD的中点.若AB=8,则EF=2.
如图,在Rt△ABC中,∠ACB=90°,点D,E分别是AB,AC的中点,点F是AD的中点.若AB=8,则EF=2.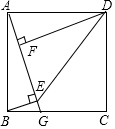 如图,正方形ABCD中,G为BC边上一点,BE⊥AG于E,DF⊥AG于F,连接DE.
如图,正方形ABCD中,G为BC边上一点,BE⊥AG于E,DF⊥AG于F,连接DE.