题目内容
已知抛物线y=2x2-6x+m的图象不在x轴的下方，则m的取值范围是 ．
考点：抛物线与x轴的交点
专题：
分析：由抛物线y=2x2-6x+m可知开口向上，与x轴没有交点，即方程2x2-6x+m=0在实数范围内没有解，由此可求出m的取值范围．
解答：解：∵抛物线y=2x2-6x+m的图象不在x轴的下方，开口向上，
∴与x轴没有交点，
方程2x2-6x+m=0在实数范围内没有解；
即b2-4ac≤0；
∴m≥
，
故答案为m≥
．
∴与x轴没有交点，
方程2x2-6x+m=0在实数范围内没有解；
即b2-4ac≤0；
∴m≥
| 9 |
| 2 |
故答案为m≥
| 9 |
| 2 |
点评：本题考查了函数与方程的关系，关键是掌握二次函数y=ax2+bx+c系数符号的确定．
练习册系列答案
快乐5加2金卷系列答案
相关题目
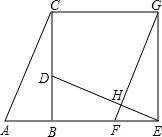如图，已知Rt△ABC中，∠ABC=90°，先把△ABC绕点B顺时针旋转90°至△DBE后，再把△ABC沿射线平移至△FEG，DE、FG相交于点H．
如图，⊙O的半径为3，P是CB延长线上一点，PO=5，PA切⊙O于A点，则PA=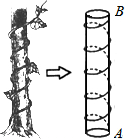
我国古代有这样一道数学问题：“枯木一根直立地上，高二丈，周三尺，有葛藤自根缠绕而上，五周而达其顶，问葛藤之长几何？”题意是：如图所示，把枯木看作一个圆柱体，因一丈是十尺，则该圆柱的高为20尺，底面周长为3尺，有葛藤自点A处缠绕而上，绕五周后其末端恰好到达点B处，则问题中葛藤的最短长度是
如图，将边长为6的正方形ABCD折叠，使点D落在AB边的中点E处，折痕为FH，点C落在点Q处，EQ与BC交于点G，则△EBG的周长是