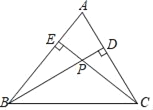
题目内容
【题目】如图![]() ,
,![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,将
,将![]() 绕着点
绕着点![]() 旋转一定的角度,得到
旋转一定的角度,得到![]() .
.
(1)若点![]() 为
为![]() 边上中点,连接
边上中点,连接![]() ,则线段
,则线段![]() 的范围为________.
的范围为________.
(2)如图![]() ,当
,当![]() 直角顶点
直角顶点![]() 在
在![]() 边上时,延长
边上时,延长![]() ,交
,交![]() 边于点
边于点![]() ,请问线段
,请问线段![]() 、
、![]() 、
、![]() 具有怎样的数量关系,请写出探索过程.
具有怎样的数量关系,请写出探索过程.
【答案】(1)![]() ;(2)AG+EG=DE,理由见解析.
;(2)AG+EG=DE,理由见解析.
【解析】
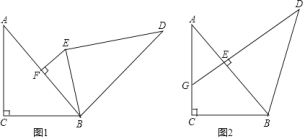
(1)图1中,利用旋转的性质得BE=BC=3,再根据三角形三边的关系得BE-BF≤EF≤BE+BF(当且仅当B、E、F共线时取等号),从而得到线段EF的范围;(2)图2中,利用旋转的性质得BE=BC=3,BD=BA=5,DE=AC=4,∠A=∠D,再判断△AGE∽△DEB,然后利用相似比计算出AG、EG,从而可得到线段DE、EG、AG的数量关系.
(1)∵点F为AB边上中点,
∴BF=2.5,
∵△ABC绕着点B旋转一定的角度得到△DEB,
∴BE=BC=3,
∵BE-BF≤EF≤BE+BF(当且仅当B、E、F共线时取等号),
∴0.5≤EF≤5.5,
故答案为0.5≤EF≤5.5;
(2)![]() .
.
理由如下:
∵![]() 绕着点
绕着点![]() 旋转一定的角度得到
旋转一定的角度得到![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目