题目内容

【题目】如图所示，在平面直角坐标系中，A（﹣1，4），B（﹣3，3），C（﹣2，1）

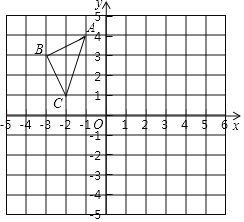
（1）已知△A′B′C′与△ABC关于x轴对称，画出△A′B′C′，并写出以下各点坐标：A′　 　；B′　 　；C′　 　．

（2）在y轴上作出点P（在图中显示作图过程），使得PA+PC的值最小，并写出点P的坐标　 　．

【答案】（1）（﹣1，﹣4）、（﹣3，﹣3）、（﹣2，﹣1）；（2）（0，3）．

【解析】

（1）分别作出三个顶点关于x轴的对称点，再首尾顺次连接可得答案；
（2）作点C关于y轴的对称点C″，连接AC″，与y轴的交点即为所求点P．

解：（1）如图所示，△A′B′C′即为所求．

由图知A′（﹣1，﹣4）、B′（﹣3，﹣3），C′（﹣2，﹣1），

故答案为：（﹣1，﹣4）、（﹣3，﹣3）、（﹣2，﹣1）；

（2）如图所示，点P即为所求，其坐标为（0，3），

故答案为：（0，3）．

练习册系列答案
相关题目

【题目】如图，小李从市场上买回一块矩形铁皮，他将此矩形铁皮的四个角各剪去一个边长为1米的正方形后，剩下的部分刚好能围成一个容积为35 m3的无盖长方体箱子，且此长方体箱子的底面长比宽多2m，现己知购买这种铁皮每平方米需30元钱，问小李购回这张矩形铁皮共花了多少元钱?

【题目】如图，直线y=﹣x+c与x轴交于点A（3，0），与y轴交于点B，抛物线y=﹣x2+bx+c经过点A，B．

（1）求点B的坐标和抛物线的解析式；

（2）M（m，0）为x轴上一动点，过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P，N．

①点M在线段OA上运动，若以B，P，N为顶点的三角形与△APM相似，求点M的坐标；

②点M在x轴上自由运动，若三个点M，P，N中恰有一点是其它两点所连线段的中点（三点重合除外），则称M，P，N三点为“共谐点”．请直接写出使得M，P，N三点成为“共谐点”的m的值．

【题目】如图，中，，，，，将绕着点旋转一定的角度，得到.

（1）若点为边上中点，连接，则线段的范围为________.

（2）如图，当直角顶点在边上时，延长，交边于点，请问线段、、具有怎样的数量关系，请写出探索过程．

【题目】如图，已知：四边形ABCD中，对角线BD平分∠ABC，∠ACB＝74°，∠ABC＝46°，且∠BAD+∠CAD＝180°，那么∠BDC的度数为_____．

【题目】如图1，已知CF是△ABC的外角∠ACE的角平分线，D为CF上一点，且DA＝DB．

（1）求证：∠ACB＝∠ADB；

（2）求证：AC+BC＜2BD；

（3）如图2，若∠ECF＝60°，证明：AC＝BC+CD．

【题目】抛物线与轴相交于、两点（其中为坐标原点），过点作直线轴于点，交抛物线于点，点关于抛物线对称轴的对称点为（其中、不重合），连接交轴于点，连接和．

（1）时，求抛物线的解析式和的长；

如图时，若，求的值．

【题目】如图，线段AB 是⊙O的直径，弦CD⊥AB于点H，点M是弧CBD 上任意一点，AH=2，CH=4．

（1）求⊙O 的半径r 的长度；

（2）求sin∠CMD；

（3）直线BM交直线CD于点E，直线MH交⊙O 于点 N，连接BN交CE于点 F，求HEHF的值．

【题目】如图，在平面直角坐标系中，抛物线y=ax2+bx+c的顶点坐标为（2，9），与y轴交于点A（0，5），与x轴交于点E、B．

（1）求二次函数y=ax2+bx+c的表达式；

（2）过点A作AC平行于x轴，交抛物线于点C，点P为抛物线上的一点（点P在AC上方），作PD平行于y轴交AB于点D，问当点P在何位置时，四边形APCD的面积最大？并求出最大面积；

（3）若点M在抛物线上，点N在其对称轴上，使得以A、E、N、M为顶点的四边形是平行四边形，且AE为其一边，求点M、N的坐标．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网