题目内容
2．已知x，y满足|x-$\sqrt{\frac{1}{4}}$|+（y+5）2=0，求2x-$\frac{8}{5}$y的值．分析 根据非负数的性质列出方程求出x、y的值，代入所求代数式计算即可．
解答 解：根据题意得：x-$\sqrt{\frac{1}{4}}$=0且y+5=0，
解得：x=$\frac{1}{2}$，y=-5．
则原式=1-$\frac{8}{5}$×（-5）=1+8=9．
点评 本题考查了非负数的性质：几个非负数的和为0时，这几个非负数都为0．
练习册系列答案
相关题目
12．等式$\frac{3x+1}{4}$-1=2x的下列变形属于等式性质2的变形是（ ）
| A． | $\frac{3x+1}{4}$=2x+1 | B． | $\frac{3x+1}{4}$-2x=1 | C． | 3x+1-4=8x | D． | $\frac{3}{4}$x+$\frac{1}{4}$-1=2x |
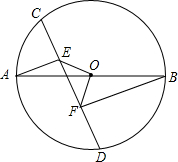如图：在⊙O中，AB是直径，CD是弦，$\widehat{AD}$=$\widehat{BD}$，过点A、B两点分别作CD的垂线，垂足分别是点E、F．连接OE，OF，求证：△OEF是等腰直角三角形．
如图，在Rt△ABC中，∠C=90°，AE=ED=DB，DG⊥AC于点G，EF⊥BC于点F，求证：四边形DFGE是菱形．