Question

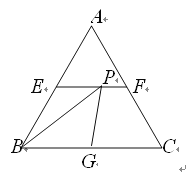
【题目】如图，在△ABC中，AB＝AC，AD⊥BC于点D,则下列四个结论中：

①线段AD上任意一点到点B的距离与到点C的距离相等;

②线段AD上任意一点到AB的距离与到AC的距离相等;

③若点Q是线段AD的三等分点 ,则△ACQ的面积是△ABC面积的;

④若,则;

正确结论的序号是（ ）

A.①②③B.①②④C.①③④D.②③④

Answer 1

【答案】B

【解析】

先根据等腰三角形三线合一的性质得出AD是BC的中垂线，再由中垂线的性质可判断①正确；

先根据等腰三角形三线合一的性质得出AD是角平分线，根据角平分线的性质可判断②正确；

根据等腰三角形三线合一的性质得出AD是BC的中线，得到△ADC的面积=△ABC的面积的，若点Q是线段AD的三等分点，则△ACQ的面积是△ADC面积的或，进而得到△ACQ的面积是△ABC面积的或，从而可判断③错误；

根据等腰三角形三线合一的性质得出AD是BC的中垂线，得出∠CAD=30°，由30°角所对直角边等于斜边的一半，即可判断④正确．

∵AB=AC，AD⊥BC，∴AD是∠BAC的平分线，BD=CD，∴线段AD上任一点到点C、点B的距离相等，∴①正确；

∵AB=AC，AD⊥BC，∴AD是∠BAC的平分线，∴AD上任意一点到AB、AC的距离相等，②正确；

∵AB=AC，AD⊥BC，∴AD是∠BAC的平分线，BD=CD，∴△ADC的面积=△ABC的面积的，若点Q是线段AD的三等分点，则△ACQ的面积是△ADC面积的或，∴△ACQ的面积是△ABC面积的或，∴③错误；

∵AB=AC，AD⊥BC，∴AD是∠BAC的平分线，BD=CD．

∵AB=AC，∴∠B=∠C．

∵∠B=60°，∴∠C=60°，∴∠CAD=30°，∴CD=AC，∴BD=AC，∴④正确．

故选B．