题目内容
一个梯形的上底与高相等,下底比上底的2倍还多1,面积是40,求它的中位线的长.
考点:梯形中位线定理
专题:
分析:设这个梯形的上底为x,则高为x,下底为2x+1,根据梯形的面积是40列出方程,解方程求出x的值,然后根据梯形中位线定理即可求出它的中位线长.
解答:解:设这个梯形的上底为x,则高为x,下底为2x+1,根据题意得
(x+2x+1)x=40,
解得x1=5,x2=-
(不合题意舍去),
所以它的中位线的长为
(x+2x+1)=
(3x+1)=
(3×5+1)=8.
| 1 |
| 2 |
解得x1=5,x2=-
| 16 |
| 3 |
所以它的中位线的长为
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了梯形中位线定理:梯形的中位线平行于两底,并且等于两底和的一半.同时考查了梯形的面积公式.

练习册系列答案
相关题目
 如图,在梯形ABCD中,AB∥CD∥MN,求证:OM=ON.
如图,在梯形ABCD中,AB∥CD∥MN,求证:OM=ON.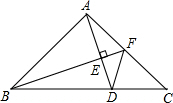 已知△ABC,AB=AC,∠BAC=90°,点F在AC上,BF⊥AD垂足为E.若DE=2,∠AFB=∠CFD,则△ADF的面积为
已知△ABC,AB=AC,∠BAC=90°,点F在AC上,BF⊥AD垂足为E.若DE=2,∠AFB=∠CFD,则△ADF的面积为