题目内容
边长为2
的正三角形与半径为1的圆最多有 个公共点.
| 3 |
考点:直线与圆的位置关系
专题:
分析:因为三角形三边长分别为2
,所以内切圆的半径为1与已知圆的半径相等,所以半径为1的圆有一个位置刚好为三角形的内切圆即与圆有三个交点,然后移动圆的位置得到四个交点,但不会出现五个交点,故得到答案.
| 3 |
解答:解:因为边长为2
的正三角形,
则内切圆的半径为1;
所以对于半径为1的圆有一个位置是正好是三角形的内切圆,
此时只有三个交点,
对于圆的位置稍向右移或其他的变化,能实现4个交点的情况,但5个以上的交点不能实现.
故答案为4.
| 3 |
则内切圆的半径为1;
所以对于半径为1的圆有一个位置是正好是三角形的内切圆,
此时只有三个交点,
对于圆的位置稍向右移或其他的变化,能实现4个交点的情况,但5个以上的交点不能实现.
故答案为4.
点评:此题很好地考查了平面几何的知识,全面而不失灵活,考查的方法上面的要求平实而不失灵动,既有切线与圆的位置,也有圆的移动.

练习册系列答案
相关题目
下列语句中,不正确的是( )
| A、位似的图形都是相似的图形 |
| B、相似的图形都是位似的图形 |
| C、位似图形的位似比等于相似比 |
| D、位似中心可以在两个图形外部,也可以在两个图形内部 |
 一条铁路MN穿过公路OA.问:在铁路MN上的何处建一个货物中转站到公路OA、OB的距离相等?请在图中画出这个点.
一条铁路MN穿过公路OA.问:在铁路MN上的何处建一个货物中转站到公路OA、OB的距离相等?请在图中画出这个点. 如图:
如图: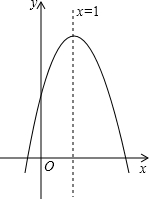 二次函数y=ax2+bx+c(a≠0)的图象如图所示,对于下列结论:①a<0;②b<0;③c>0;④2a+b=0;⑤a-b+c<0,其中正确的个数是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,对于下列结论:①a<0;②b<0;③c>0;④2a+b=0;⑤a-b+c<0,其中正确的个数是( ) 如图,⊙O的两弦AB,CD垂直相交于点E,试判断∠AOC与∠?BOD的关系并给出证明.
如图,⊙O的两弦AB,CD垂直相交于点E,试判断∠AOC与∠?BOD的关系并给出证明. 已知,如图,AD∥BC,∠1=∠2,∠3=∠E.试说明:AE∥CD.
已知,如图,AD∥BC,∠1=∠2,∠3=∠E.试说明:AE∥CD.