题目内容
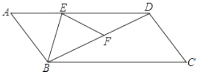
【题目】边长为4、中心为
的正方形
如图所示，动点
从点
出发，沿
以每秒1个单位长度的速度运动到点时停止，动点
从点出发，沿
以每秒2个单位长度的速度运动一周停止，若点
同时开始运动，点的运动时间为
，当
时，满足
的点的位置有（ ）
A.6个B.7个C.8个D.9个
【答案】B
【解析】
依次取
的中点
，连接
．由题意可知，当点
与点
到各自所在边的中点的距离相等时，
，则有六种情况，分类列式计算求出t的值，即可解答本题．
解：依次取的中点，连接．
根据题意，得点运动的路程为
，当
时，点运动的路程为
．
分析题意可知，当点与点到各自所在边的中点的距离相等时，．
当时，显然
；
②当
时，如图（1），点在
上，点在
上，
，
由
，得
；
③当
时，如图（2），点在
上，点在
上，
，
由
，得
或
；
④当
时，如图（3），点在
上，点在
上，
，
由
，得（舍去）或
；
⑤当
时，如图（4），点在
上，点在
上，
，
由
，得
或
；
⑥当
时，点停在点
处，因此当
时，
，只有
时满足
．
综上，满足条件
的点的位置有7个，
故选：B．
优质课堂快乐成长系列答案【题目】某果品超市经销一种水果，已知该水果的进价为每千克15元，通过一段时间的销售情况发现，该种水果每周的销售总额相同，且每周的销售量
(千克)与每千克售价
(元)的关系如表所示：
每千克售价 | 25 | 30 | 40 |
每周销售量 | 240 | 200 | 150 |
（1）求出每周销售量(千克)与每千克售价(元)的函数关系式．
（2）由于销售淡季即将来临，超市要完成每周销售量不低于300千克的任务，则该种水果每千克售价最多定为多少元？
（3）在（2）的基础上，超市销售该种水果能否达到每周获利2000元？说明理由．
【题目】有这样一个问题探究函数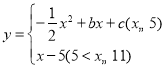
（b、c为常数）的图象和性质．元元根据学习函数的经验，对该函数的图象和性质进行了以下探究：
下面是元元的探究过程，请你补充完整
x | …… | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | …… |
y | …… | 0 | 2.5 | 4 | m | 4 | 2.5 | 0 | 1 | …… |
（1）根据上表信息，其中b＝____，c＝_____，m＝______．
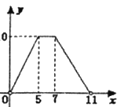
（2）如图，在下面平面直角坐标系中，描出以补全后的表中各对应值为坐标的点，并画出该函数的另一部分图象；
（3）观察函数图象，请写出该函数的一条性质：______．
（4）解决问题：若直线y＝3n+2（n为常数）与该函数图象有3个交点时，求n的范围．
