题目内容
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 与点
与点![]() 关于
关于![]() 轴对称,点
轴对称,点![]() 的坐标为
的坐标为![]() ,过点
,过点![]() 作
作![]() 轴的垂线
轴的垂线![]() 交抛物线于点
交抛物线于点![]() .
.
(1)求点![]() 、点
、点![]() 、点
、点![]() 的坐标;
的坐标;
(2)当点![]() 在线段
在线段![]() 上运动时,直线
上运动时,直线![]() 交
交![]() 于点
于点![]() ,试探究当
,试探究当![]() 为何值时,四边形
为何值时,四边形![]() 是平行四边形;
是平行四边形;
(3)在点![]() 的运动过程中,是否存在点
的运动过程中,是否存在点![]() ,使
,使![]() 是以
是以![]() 为直角边的直角三角形?若存在,求出点
为直角边的直角三角形?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]()
(2)当![]() ,四边形
,四边形![]() 是平行四边形
是平行四边形
(3)存在,点![]() 的坐标为
的坐标为![]() ,
,![]() ,
,![]()
【解析】
(1)根据函数解析式列方程即可;
(2)根据平行四边形的判定,用含未知数的值表示QM的长度,从而可求解;
(3)设Q点的坐标为![]() ,分两种情况讨论:
,分两种情况讨论:![]() 当
当![]() 时,由勾股定理可得:
时,由勾股定理可得:![]() ,
,![]() 当
当![]() 时,由勾股定理可得:
时,由勾股定理可得:![]() ,可解出
,可解出![]() 的值.
的值.
(1)令![]() ,则
,则![]() ,C点的坐标为(0,2);
,C点的坐标为(0,2);
令![]() ,则
,则![]() 解得
解得![]() ,点A为(-1,0);点B为(4,0)
,点A为(-1,0);点B为(4,0)
∴![]()
(2)如图1所示:
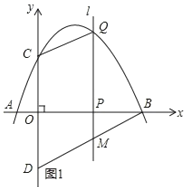
点C与点D关于![]() 轴对称,点
轴对称,点![]() ,设直线BD的解析式为
,设直线BD的解析式为![]() ,将
,将![]() 代入得:
代入得:![]() 解得
解得![]()
∴直线BD的解析式为:![]()
∵![]()
∴当![]() 时,四边形
时,四边形![]() 是平行四边形
是平行四边形
设Q点的坐标为![]() ,则
,则![]()
∴![]()
解得![]()
![]() (不合题意,舍去)
(不合题意,舍去)
∴当![]() ,四边形
,四边形![]() 是平行四边形
是平行四边形
(3)存在,设Q点的坐标为![]()
∵![]() 是以BD为直角边的直角三角形
是以BD为直角边的直角三角形
∴![]() 当
当![]() 时,由勾股定理可得:
时,由勾股定理可得:![]()
即![]()
解得![]()
![]() (不合题意,舍去)
(不合题意,舍去)
∴Q点的坐标为![]()
![]() 当
当![]() 时,由勾股定理可得:
时,由勾股定理可得:![]()
即![]()
解得![]()
![]()
Q点的坐标为![]()
![]()
综上所述:点![]() 的坐标为
的坐标为![]() ,
,![]() ,
,![]() .
.

 高中必刷题系列答案
高中必刷题系列答案【题目】问题呈现:我们知道反比例函数y=![]() (x>0)的图象是双曲线,那么函数y=
(x>0)的图象是双曲线,那么函数y=![]() +n(k、m、n为常数且k≠0)的图象还是双曲线吗?它与反比例函数y=
+n(k、m、n为常数且k≠0)的图象还是双曲线吗?它与反比例函数y=![]() (x>0)的图象有怎样的关系呢?让我们一起开启探索之旅……
(x>0)的图象有怎样的关系呢?让我们一起开启探索之旅……
探索思考:我们可以借鉴以前研究函数的方法,首先探索函数y=![]() 的图象.
的图象.
(1)填写下表,并画出函数y=![]() 的图象.
的图象.
①列表:
x | … | ﹣5 | ﹣3 | ﹣2 | 0 | 1 | 3 | … |
y | … | … |
②描点并连线.
(2)观察图象,写出该函数图象的两条不同类型的特征:
① ② ;
理解运用:函数y=![]() 的图象是由函数y=
的图象是由函数y=![]() 的图象向 平移 个单位,其对称中心的坐标为 .
的图象向 平移 个单位,其对称中心的坐标为 .
灵活应用:根据上述画函数图象的经验,想一想函数y=![]() +2的图象大致位置,并根据图象指出,当x满足 时,y≥3.
+2的图象大致位置,并根据图象指出,当x满足 时,y≥3.

【题目】电影《我和我的祖国》上映以来好评如潮,某影评平台随机调查了部分观众对这部电影的评分(满分10分),并将调查结果制成了如下不完整的统计图表(表中每组数据不包括最小值,包括最大值):
等级 | 频数 | 频率 |
A等(9.6分~10分) | a | 0.7 |
B等(8.8分~9.6分) | 3 | 0.15 |
C等(8.2分~8.8分) | b | c |
D等(8.2分及以下) | 1 | 0.05 |
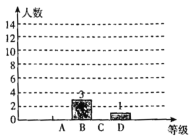
请根据图表信息,解答下列问题:
(1)这次共随机调查了_______名观众,a=______;b=______;c=______;
(2)补全条形统计图;
(3)若某电影院同时上映《我和我的祖国》、《中国机长》和《烈火英雄》,红红和兰兰分别选择其中一部电影观看,求她们选中同一部电影的概率.