题目内容
18.因式分解:(1)x2-2x-8=(x+2)(x-4);
(2)-a4+16;
(3)3a3(1-2a)+a(2a-1)2+2a(2a-1).
分析 根据因式分解的方法即可求出答案.
解答 解:(1)原式=(x+2)(x-4)
(2)原式=16-a4=(4+a2)(4-a2)=(4+a2)(2+a)(2-a)
(3)原式=3a3(1-2a)+a(1-2a)3-2a(1-2a)
=a(1-2a)(3a2+1-2a-2)
=a(1-2a)(a-1)(3a+1)
故答案为:(1)(x+2)(x-4)
点评 本题考查因式分解,涉及提取公因式,公式法,属于基础题型.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
3. 如图,AE∥DF,AE=DF,则添加下列条件还不能使△EAC≌△FDB的为( )
如图,AE∥DF,AE=DF,则添加下列条件还不能使△EAC≌△FDB的为( )
 如图,AE∥DF,AE=DF,则添加下列条件还不能使△EAC≌△FDB的为( )
如图,AE∥DF,AE=DF,则添加下列条件还不能使△EAC≌△FDB的为( )| A. | AB=CD | B. | CE∥BF | C. | ∠E=∠F | D. | CE=BF |
10.二次函数y=(x+1)2-4的顶点坐标是( )
| A. | (-1,-4) | B. | (1,4) | C. | (1,-4) | D. | (-1,4) |
8.已知$\frac{a}{b}=\frac{7}{5}$,则$\frac{a-b}{b}$的值为( )
| A. | $\frac{2}{7}$ | B. | $\frac{7}{2}$ | C. | $\frac{5}{2}$ | D. | $\frac{2}{5}$ |
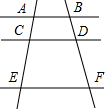 如图,AB∥CD∥EF,若$\frac{AC}{CE}$=$\frac{1}{2}$,则$\frac{BD}{BF}$=$\frac{1}{3}$.
如图,AB∥CD∥EF,若$\frac{AC}{CE}$=$\frac{1}{2}$,则$\frac{BD}{BF}$=$\frac{1}{3}$.