题目内容
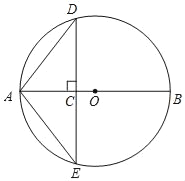
【题目】如图所示是一张简易活动餐桌,测得OA=OB=30cm,OC=OD=50cm,现要求桌面离地面的高度为40cm,那么两条桌脚的张角∠COD的度数大小应为( )
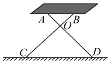
A. 100° B. 120° C. 135° D. 150°
【答案】B
【解析】
连接CD,过O作NM⊥CD,交AB于N,交CD于M,推出MN⊥AB,推出△ABO∽△DCO,得出比例式,求出OM,根据含30度角的直角三角形性质求出∠C=∠D=30°,求出∠COM和∠DOM即可.
解:连接CD,过O作NM⊥CD,交AB于N,交CD于M,

∵AB∥CD,
∴MN⊥AB,
∵AB∥CD,
∴△ABO∽△DCO,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,解得:OM=25,
,解得:OM=25,
∵CO=50,
∴MO=![]() CO,
CO,
∴∠C=30°,
∴∠COM=90°-30°=60°,
同理∠DOM=60°,
∴∠COD=60°+60°=120°,
故选:B.

【题目】下表显示了同学们用计算机模拟随机投针实验的某次实验的结果.
投针次数n | 1000 | 2000 | 3000 | 4000 | 5000 | 10000 | 20000 |
针与直线相交的次数m | 454 | 970 | 1430 | 1912 | 2386 | 4769 | 9548 |
针与直线相交的频率p=
| 0.454 | 0.485 | 0.4767 | 0.478 | 0.4772 | 0.4769 | 0.4774 |
下面有三个推断:
①投掷1000次时,针与直线相交的次数是454,针与直线相交的概率是0.454;
②随着实验次数的增加,针与直线相交的频率总在0.477附近,显示出一定的稳定性,可以估计针与直线相交的概率是0.477;
③若再次用计算机模拟此实验,则当投掷次数为10000时,针与直线相交的频率一定是0.4769.
其中合理的推断的序号是:_____.
【题目】如图,⊙O的直径AB=4cm,点C为线段AB上一动点,过点C作AB的垂线交⊙O于点D,E,连结AD,AE.设AC的长为xcm,△ADE的面积为ycm2.
小东根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.
下面是小东的探究过程,请补充完整:
(1)确定自变量x的取值范围是 ;
(2)通过取点、画图、测量、分析,得到了y与x的几组对应值,如下表:
x/cm | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
y/cm2 | 0 | 0.7 | 1.7 | 2.9 |
| 4.8 | 5.2 | 4.6 | 0 |
(3)如图,建立平面直角坐标系xOy,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;
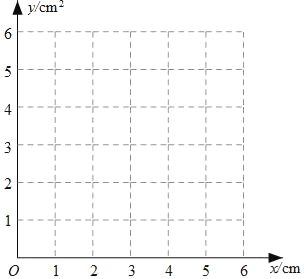
(4)结合画出的函数图象,解决问题:当△ADE的面积为4cm2时,AC的长度约为 cm.