Question

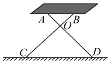
【题目】如图，已知，正方形ABCD和一个圆心角为45°的扇形，圆心与A点重合，此扇形绕A点旋转时，两半径分别交直线BC、CD于点P．K．

（1）当点P、K分别在边BC．CD上时，如图（1），求证：BP+DK＝PK．

（2）当点P、K分别在直线BC．CD上时，如图（2），线段BP、DK、PK之间又有怎样的数量关系，请直接写出结论．

（3）在图（3）中，作直线BD交直线AP、AK于M、Q两点．若PK＝5，CP＝4，求PM的长．

Answer 1

【答案】（1）证明见解析；（2）BP＝DK+PK，理由见解析；（3）PM的长是．

【解析】

（1）延长CD到N，使DN=BP，连接AN，根据正方形的性质和全等三角形的判定SAS证△ABP≌△ADN，推出AN=AP，∠NAD=∠PAB，求出∠NAK=∠KAP=45°，根据SAS证△NAK和△KAP全等即可；
（2）在BC上截取BN=DK，连接AN，与（1）类似证△ADK≌△ABN和△KAP≌△NAP，推出BN=DK，NP=PK即可；
（3）在DC上截取DN=BP，连接AN，与（1）类似证△ADN≌△ABP和△KAP≌△KAN，推出BP=DN，NK=PK，得出DK=PB+PK，求出正方形的边长，根据勾股定理求出AN、AK、AP，求出∠ABM=∠ACK=135°，∠PAB=∠CAK，证△MAB和△KAC相似，得出比例式，代入求出即可．

（1）证明：延长CD到N，使DN＝BP，连接AN，

∵正方形ABCD，

∴∠ABP＝∠ADC＝90°＝∠BAD，AD＝AB，

∴∠ADN＝90°＝∠ABP，

在△ABP和△ADN中

,

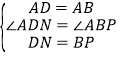∴△ABP≌△ADN，

∴AN＝AP，∠NAD＝∠PAB，

∵∠BAD＝90°，∠PAK＝45°，

∴∠BAP+∠KAD＝45°，

∴∠NAD+∠DAK＝45°，

即∠NAK＝∠KAP＝45°，

在△NAK和△KAP中

,

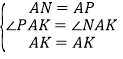∴△PAK≌△NAK，

∴NK＝KP，

∴BP+DK＝PK．

（2）解：BP＝DK+PK，

理由是：在BC上截取BN＝DK，连接AN，

与（1）类似△ADK≌△ABN，

∴AK＝AN，∠KAD＝∠BAN，

∵∠KAP＝45°，

∴∠NAB+∠DAP＝45°，

∴∠NAP＝90°﹣45°＝45°＝∠KAP，

与（1）类似△KAP≌△NAP（SAS），

∴PK＝PN，

∴BP＝BN+NP＝DK+PK，

即BP＝DK+PK．

（3）解：在△CPK中，CP＝4，PK＝5，由勾股定理得：CK＝3，

在DC上截取DN＝BP，连接AN，

由（1）可知：AN＝AP，

与（2）证法类似△NAK≌△PAK，

∴PK＝NK，

∴DK＝PB+PK，

即DC+3＝4﹣BC+5，

∵正方形ABCD，DC＝BC，

解得：AD＝DC＝BC＝AB＝3，

连接AC，

∵正方形ABCD，

∴∠ACB＝∠DBC＝∠MBP＝45°，

∵∠ABC＝∠PCK＝90°，

∴∠ABM＝∠ACK＝45°+90°＝135°，

在Rt△ABC中，由勾股定理得：AC＝3，

在Rt△ABP中，由勾股定理得：AP＝＝，

在Rt△ADK中，由勾股定理得：AK＝＝3，

∵∠PAK＝∠BAC＝45°，∠BAK＝∠BAK，

∴∠PAB＝∠KAC，

∵∠ABM＝∠ACK，

∴△MAB∽△KAC，

∴，

即＝，

解得：PM＝，

答：PM的长是．