题目内容
 如图,在△ABC中,AB=AC,点D、E在BC上,连接AD、AE,如果只添加一个条件,使得∠DAB=∠EAC,则添加的条件不能为( )
如图,在△ABC中,AB=AC,点D、E在BC上,连接AD、AE,如果只添加一个条件,使得∠DAB=∠EAC,则添加的条件不能为( )| A、AD=DE |
| B、BD=CE |
| C、AD=AE |
| D、BE=CD |
考点:全等三角形的判定与性质
专题:
分析:分别根据每个选项给出条件求证∠DAB=∠EAC,不能得出结论的即为正确选项.
解答:解:A、不能证明,故A错误;
B、∵AB=AC,∴∠B=∠C,
∵在△ABD和△ACE中,
,
∴△ABD≌△ACE,(SAS)
∴∠DAB=∠EAC;故B正确;
C、∵AD=AE,
∴∠ADE=∠AED,
∵AB=AC,
∴∠B=∠C,
∵∠ADE=∠BAD+∠B,∠AED=∠CAE+∠C,
∴∠DAB=∠EAC,故C正确;
D、∵BE=CD,
∴BD=CE,
∵AB=AC,∴∠B=∠C,
∵在△ABD和△ACE中,
,
∴△ABD≌△ACE,(SAS)
∴∠DAB=∠EAC;故D正确;
故选 A.
B、∵AB=AC,∴∠B=∠C,
∵在△ABD和△ACE中,
|
∴△ABD≌△ACE,(SAS)
∴∠DAB=∠EAC;故B正确;
C、∵AD=AE,
∴∠ADE=∠AED,
∵AB=AC,
∴∠B=∠C,
∵∠ADE=∠BAD+∠B,∠AED=∠CAE+∠C,
∴∠DAB=∠EAC,故C正确;
D、∵BE=CD,
∴BD=CE,
∵AB=AC,∴∠B=∠C,
∵在△ABD和△ACE中,
|
∴△ABD≌△ACE,(SAS)
∴∠DAB=∠EAC;故D正确;
故选 A.
点评:本题考查了全等三角形的判定,考查了全等三角形对应角相等的性质,本题中求证△ABD≌△ACE是解题的关键.

练习册系列答案
相关题目
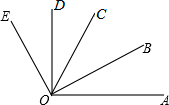 如图,OB是∠AOC的角平分线,OD是∠COE的角平分线.
如图,OB是∠AOC的角平分线,OD是∠COE的角平分线. 如图,过⊙O内一点P作弦AB、CD,且AB=CD,在
如图,过⊙O内一点P作弦AB、CD,且AB=CD,在