题目内容
【题目】定义：对于给定的两个函数,任取自变量x的一个值,当x<0时,它们对应的函数值互为相反数;当x0时,它们对应的函数值相等,我们称这样的两个函数互为相关函数。例如：一次函数y=x1,它们的相关函数为y=
.
(1)已知点A(5,8)在一次函数y=ax3的相关函数的图象上，求a的值；
(2)已知二次函数y=x
+4x
.
①当点B(m,
)在这个函数的相关函数的图象上时，求m的值；
②当3x3时,求函数y=x+4x的相关函数的最大值和最小值.
【答案】（1）1；（2）①m=2
或m=2+
或m=2 ；②最大值为
,最小值为
.
【解析】
（1）写出y=ax-3的相关函数，代入计算；
（2）①写出二次函数y=x
+4x的相关函数，代入计算；
②根据二次根式的最大值和最小值的求法解答．
(1)y=ax3的相关函数y=
，
将A(5,8)代入y=ax+3得：5a+3=8，
解得a=1；
(2)二次函数y=x+4x的相关函数为y=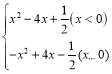
，
①当m<0时,将B(m, 
)代入y=x-4x+
得m-4m+
，
解得：m=2+ (舍去),或m=2，
当m0时,将B(m, )代入y=x+4x得：
m +4m ，
解得：m=2+
或m=2.
综上所述：m=2 或m=2+或m=2 ；
②当3x<0时, y=x+4x，抛物线的对称轴为x=2，
此时y随x的增大而减小，
∴此时y的最大值为，
当0x3时,函数y=x+4x，抛物线的对称轴为x=2，
当x=0有最小值,最小值为,当x=2时,有最大值,最大值y=
，
综上所述,当3x3时,函数y=x+4x的相关函数的最大值为 ,最小值为.
【题目】某班“数学兴趣小组”对函数
的图象和性质进行了探究，探究过程如下：
（
）自变量
的取值范围是全体实数，与
的几组对应值如下表：
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
其中，
__________．
（
）根据表中数据，在如图所示的平面直角坐标系中描点，并画出了函数图象的一部分，请你画出该函数图象剩下的部分．
（
）观察函数图象，写出一条性质__________．
（
）进一步探究函数图象发现：
①方程
有__________个实数根．
②关于的方程
有个实数根时，
的取值范围是__________．
【题目】某公司有A型产品40件，B型产品60件，分配给下属甲、乙两个商店销售，其中70件给甲店，30件给乙店，且都能卖完。设分配给甲店A型产品x件，两商店销售这两种产品每件的利润（元）如下表：
A型利润 | B型利润 | |
甲店 | 200 | 170 |
乙店 | 160 | 150 |
（1）分配给乙店B型产品 件（用含x的代数式表示）。
（2）设这家公司卖出这100件产品的总利润为W（元），求W关于x的函数关系式，并直接写出x的取值范围。
（3）若公司要求总利润不低于17560元，有几种不同分配方案？哪种方案总利润最大？请求出最大利润。