题目内容

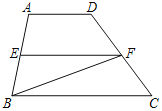
【题目】如图，在梯形ABCD中，AD∥BC，EF是梯形ABCD的中位线，若△BEF的面积为4cm2，则梯形ABCD的面积为（　　）

A.8cm2B.12cm2C.16cm2D.20cm2

【答案】C

【解析】

如图，过A作AN⊥BC于N，交EF于M，根据梯形的中位线性质得出AD+BC＝2EF，AM＝MN，由此再根据已知三角形的面积得出EF×AM＝8，由此进一步根据梯形面积公式变形求解即可．

如图，过A作AN⊥BC于N，交EF于M，

∵EF是梯形ABCD的中位线，

∴AD+BC＝2EF，EF∥AD∥BC，

∴AM⊥EF，AM＝MN，

∵△BEF的面积为4cm2，

∴EF×AM＝4，

∴EF×AM＝8，

∴梯形ABCD的面积为(AD+BC)×AN＝×2EF×2AM＝2EF×AM＝16cm2，

故选：C．

练习册系列答案
相关题目

【题目】如图，以AB为直径的⊙O交△ABC的边AC于D、BC于E，过D作⊙O的切线交BC于F，交BA延长线于G，且DF⊥BC．

（1）求证：BA＝BC；

（2）若AG＝2，cosB＝，求DE的长．

【题目】先化简，再求值：，其中x是不等式组的整数解．

【题目】如图在平面直角坐标系中，将△ABO绕点A顺时针旋转到△AB1C1的位置，点B、O分别落在点B1、C1处，点B1在x轴上，再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置，点C2在x轴上，将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置，点A2在x轴上，依次进行下去…若点A（，0），B（0，2），则点B2018的坐标为（　　）

A. （6048，0）B. （6054，0）C. （6048，2）D. （6054，2）

【题目】如图，一次函数yx3的图象与反比例函数y(k为常数，且k0)的图象交于A（1，a），B两点．

（1）求反比例函数的表达式及点B的坐标；

（2）在x轴上找一点P，使PA+PB的值最小，求满足条件的点P的坐标．

【题目】如图，在以线段AB为直径的⊙O上取一点，连接AC、BC.将△ABC沿AB翻折后得到△ABD.

（1）试说明点D在⊙O上；

（2）在线段AD的延长线上取一点E，使AB2=AC·AE.求证：BE为⊙O的切线；

（3）在（2）的条件下，分别延长线段AE、CB相交于点F，若BC=2，AC=4，求线段EF的长.

【题目】在平面直角坐标系中，函数（）的图象经过点（4，1），直线与图象交于点，与轴交于点．

（1）求的值；

（2）横、纵坐标都是整数的点叫做整点．记图象在点，之间的部分与线段，，围成的区域（不含边界）为．

①当时，直接写出区域内的整点个数；

②若区域内恰有4个整点，结合函数图象，求的取值范围．

【题目】已知：在正方形ABCD中，点E在 BC边上，连接 DE，以DE为直角边作等腰直角三角形EDF（∠DEF=90°），过点C作 DE的垂线，垂足为G，交AB于点H，连接 FH．

（1）如图 1，求证：四边形FECH为平行四边形

（2）如图 2，连接 DH和 AF，点 E 为 BC 中点，在不添加任何辅助线与字母的情况下，请直接写出与平行四边形FECH面积相等的所有三角形．

【题目】如图，甲、乙只捕捞船同时从A港出海捕鱼，甲船以每小时15 km的速度沿北偏西60°方向前进，乙船以每小时15 km的速度沿东北方向前进．甲船航行2 h到达C处，此时甲船发现渔具丢在了乙船上，于是甲船快速(匀速)沿北偏东75°的方向追赶乙船，结果两船在B处相遇．问：

(1)甲船从C处出发追赶上乙船用了多少时间？

(2)甲船追赶乙船的速度是每小时多少千米？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网