Question

已知在Rt△ABC中，∠ACB=90°，AC=BC，BM⊥CM于M，且CM>BM

（1）如图1，过点A作AF⊥CM于F，直线写出线段BM、AF、MF的数量关系是______

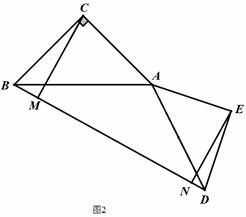
（2）如图2，D为BM延长线上一点，连AD以AD为斜边向右侧作等腰Rt△ADE，再过点E作EN⊥BM于N，求证：CM+EN=MN；

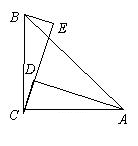
（3）将（2）中的△ADE绕点A顺时针旋转任意角a后，连BD取BD中点P，连CP、EP，作出图形，试判断CP、EP的数量和位置关系并证明

 

Answer 1

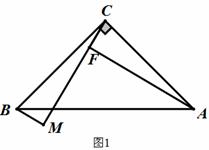
解：(1) AF＝BM＋MF

    (2) 过点A作AG⊥CM于G，反向延长GA交EN于H

    ∴四边形GMNH为矩形

    ∴AH⊥EN

    根据三垂直得：△CMB≌△AGC，△AEH≌△EDN

    ∴CM＝AG，EN＝AH

    ∴MN＝GH＝GA＋AH＝CM＋EN

    (3) 中线倍长CP，则△BCP≌△DGP

    ∴BC＝DG，BC∥DG

    可证：△CAE≌△GDE

    ∴CE＝EG，CE⊥EG

    ∴△CPE为等腰直角三角形

    ∴CP＝PE，CP⊥PE