题目内容
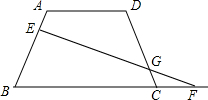 如图,已知在梯形ABCD中,AD∥BC,AD=AB=CD=5,∠ABC=60°,E是AB边上的一点
如图,已知在梯形ABCD中,AD∥BC,AD=AB=CD=5,∠ABC=60°,E是AB边上的一点| AE |
| BE |
| 2 |
| 3 |
(1)求BC的长;
(2)若点F在BC的延长线上,设CF=x,
| DG |
| CG |
(3)当CF=2时,求DG的长.
考点:梯形,相似三角形的判定与性质
专题:计算题
分析:(1)过点D作DM∥AB交BC于点M,即可得到一个平行四边形,进而得到一个等边三角形,最后求出BC的长;
(2)延长FE交DA的延长线于点O,然后根据相似三角形的性质进行解答即可;
(3)结合第二问的结论代入进行求值.
(2)延长FE交DA的延长线于点O,然后根据相似三角形的性质进行解答即可;
(3)结合第二问的结论代入进行求值.
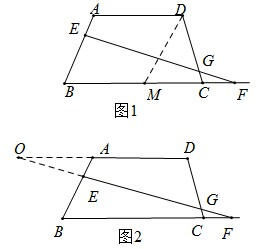
解答:解:(1)如图1所示,过点D作DM∥AB交BC于点M,
则四边形ABMD是平行四边形,
∴BM=AD=5,∠DMC=∠ABC=60°,
∵AD=AB=CD=5,
∴△CMD是等边三角形,
∴CM=CD=5,
∴BC=BM+CM=5+5=10;
(2)如图2所示,延长FE交DA的延长线于点O,
∵AD∥BC,
∴△ODG∽△FCG,
∴
=
,
∵CF=x,
=y,
∴
=y,①
∵AD∥BC,
∴△OAE∽△FBE,
∴
=
,
∵
=
,
∴
=
,
∴OA=
(10+x),②
由①②得y=
+
,
即y与x的函数关系式为
y=
+
,(x>0);
(3)当CF=2,即x=2时,y=
+
=
,
即
=
,
∵DG+CG=5,
∴DG=
.
则四边形ABMD是平行四边形,
∴BM=AD=5,∠DMC=∠ABC=60°,
∵AD=AB=CD=5,
∴△CMD是等边三角形,
∴CM=CD=5,
∴BC=BM+CM=5+5=10;
(2)如图2所示,延长FE交DA的延长线于点O,
∵AD∥BC,
∴△ODG∽△FCG,
∴
| OD |
| CF |
| DG |
| CG |
∵CF=x,
| DG |
| CG |
∴
| OD |
| x |
∵AD∥BC,
∴△OAE∽△FBE,
∴
| OA |
| BF |
| AE |
| BE |
∵
| AE |
| BE |
| 2 |
| 3 |
∴
| OA |
| 10+x |
| 2 |
| 3 |
∴OA=
| 2 |
| 3 |
由①②得y=
| 35 |
| 3x |
| 2 |
| 3 |
即y与x的函数关系式为
y=
| 35 |
| 3x |
| 2 |
| 3 |
(3)当CF=2,即x=2时,y=
| 35 |
| 3×2 |
| 2 |
| 3 |
| 13 |
| 3 |
即
| DG |
| CG |
| 13 |
| 3 |
∵DG+CG=5,
∴DG=
| 65 |
| 16 |

点评:该题目考查了等腰梯形的性质、相似三角形的判定和性质,对边三角形的判定和性质,关键是分析题意作出辅助线.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
若两个连续偶数的积是224,则这两个数的和是( )
| A、14 | B、16 | C、30 | D、32 |
 如图,在梯形ABCD中,AD∥BC,对角线AC、BD相交于点O,AD=2,BC=BD=3,AC=4.
如图,在梯形ABCD中,AD∥BC,对角线AC、BD相交于点O,AD=2,BC=BD=3,AC=4.