题目内容
5.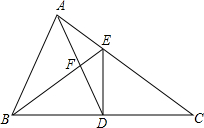 如图,△ABC中,D、E分别为BC、AC上一点,AB=AD,BE=EC.
如图,△ABC中,D、E分别为BC、AC上一点,AB=AD,BE=EC.(1)求证:△FDB∽△ABC;
(2)若AF=DF,求证:DE⊥BC.
分析 (1)根据等边对等角可知∠ABD=∠ADB,∠EBC=∠ECB,从而可证明△FDB∽△ABC;
(2)由AF=DF可知:DF=$\frac{1}{2}$AD=$\frac{1}{2}$AB,然后利用相似三角形的性质可知BD:BC=1:2,从而可知BD=DC,最后利用等腰三角形三线合一的性质可得到DE⊥BC.
解答 解:(1)∵AB=AD,BE=EC,
∴∠ABD=∠ADB,∠EBC=∠ECB.
∴△FDB∽△ABC.
(2)∵AF=DF,
∴DF=$\frac{1}{2}$AD=$\frac{1}{2}$AB,即$\frac{DF}{AB}=\frac{1}{2}$.
∵△FDB∽△ABC,
∴$\frac{BD}{BC}=\frac{DF}{AB}=\frac{1}{2}$.
∴BD=$\frac{1}{2}BC$.
∴BD=DC.
又∵EB=EC,
∴ED⊥BC.
点评 本题主要考查的是相似三角形的性质和判定、等腰三角形的性质,利用相似三角形的性质证得BD=DC是解题的关键.

练习册系列答案
相关题目
17.下面是小丽同学做的合并同类项的题,其中正确的是( )
| A. | 5ab-3ab=2 | B. | 2a+3b=5ab | C. | x2y-2x2y=-x2y | D. | a3+a2=a5 |
14.抛物线y=x2向左平移3个单位,再向下平移2个单位后,所得的抛物线表式是( )
| A. | y=(x-3)2-2 | B. | y=(x-3)2+2 | C. | y=(x+3)2-2 | D. | y=(x+3)2+2 |
15.△ABC中,BC=5,AC=7,则AB边的取值范围是( )
| A. | 1<AB<2 | B. | 4<AB<14 | C. | 2<AB<12 | D. | 4<AB<10 |
 如图所示,在△ABC中,DE∥BC交AB于点D,交AC于点E,且AE:EC=2:1,连接DC,求S△ADE:S△BDC的值.
如图所示,在△ABC中,DE∥BC交AB于点D,交AC于点E,且AE:EC=2:1,连接DC,求S△ADE:S△BDC的值.