题目内容
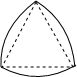如图，“凸轮”的外围由以正三角形的顶点为圆心，以正三角形的边长为半径的三段等弧组成．已知正三角形的边长为1，则凸轮的周长等于（ ）| A、π | ||
B、
| ||
| C、2π | ||
D、
|
考点：弧长的计算
专题：
分析：由“凸轮”的外围是以正三角形的顶点为圆心，以正三角形的边长为半径的三段等弧组成，得到∠A=∠B=∠C=60°，AB=AC=BC=1，然后根据弧长公式计算出三段弧长，三段弧长之和即为凸轮的周长．
解答：解：∵△ABC为正三角形，
∴∠A=∠B=∠C=60°，AB=AC=BC=1，
∴
=
=
=
=
，
根据题意可知凸轮的周长为三个弧长的和，
即凸轮的周长=
+
+
=3×
=π．
故选A．
∴∠A=∠B=∠C=60°，AB=AC=BC=1，
∴
 |
| AB |
|
| BC |
|
| AC |
| 60π×1 |
| 180 |
| π |
| 3 |
根据题意可知凸轮的周长为三个弧长的和，
即凸轮的周长=
|
| AB |
|
| BC |
|
| AC |
| π |
| 3 |
故选A．
点评：本题考查了弧长的计算以及等边三角形的性质，熟练掌握弧长公式是解本题的关键．
练习册系列答案
相关题目
如图，在Rt△ABC中，∠C=90°，则sinA的值为（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
实数4，
，2，|-3|中，最小的是（ ）
| 5 |
| A、4 | ||
B、
| ||
| C、2 | ||
| D、|-3| |
大于-
且小于
的整数有（ ）
| 2 |
| 5 |
| A、1个 | B、2个 | C、3个 | D、4个 |
