题目内容
 如图,AB与⊙O1与⊙O2分别相切于点A、B,AB与O1O2相交于点P,已知⊙O1与⊙O2的半径分别为3,6,PA=4,那么AB=________.
如图,AB与⊙O1与⊙O2分别相切于点A、B,AB与O1O2相交于点P,已知⊙O1与⊙O2的半径分别为3,6,PA=4,那么AB=________.
12
分析:首先连接O1A,O2B,由AB与⊙O1与⊙O2分别相切于点A、B,即可得O1A⊥AB,O2B⊥AB,继而证得:△APO1∽△BPO2,然后利用相似三角形的对应边成比例,即可求得答案.
解答: 解:连接O1A,O2B,
解:连接O1A,O2B,
∵AB与⊙O1与⊙O2分别相切于点A、B,
∴O1A⊥AB,O2B⊥AB,
∴O1A∥O2B,
∴△APO1∽△BPO2,
∴ ,
,
∵⊙O1与⊙O2的半径分别为3,6,PA=4,
∴ ,
,
解得:PB=8,
∴AB=PA+PB=4+8=12.
故答案为:12.
点评:此题考查了切线的性质以及相似三角形的判定与性质.此题难度适中,注意掌握辅助线的作法是解此题的关键,注意数形结合思想的应用.
分析:首先连接O1A,O2B,由AB与⊙O1与⊙O2分别相切于点A、B,即可得O1A⊥AB,O2B⊥AB,继而证得:△APO1∽△BPO2,然后利用相似三角形的对应边成比例,即可求得答案.
解答:
 解:连接O1A,O2B,
解:连接O1A,O2B,∵AB与⊙O1与⊙O2分别相切于点A、B,
∴O1A⊥AB,O2B⊥AB,
∴O1A∥O2B,
∴△APO1∽△BPO2,
∴
 ,
,∵⊙O1与⊙O2的半径分别为3,6,PA=4,
∴
 ,
,解得:PB=8,
∴AB=PA+PB=4+8=12.
故答案为:12.
点评:此题考查了切线的性质以及相似三角形的判定与性质.此题难度适中,注意掌握辅助线的作法是解此题的关键,注意数形结合思想的应用.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
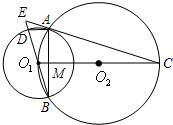 的延长线交于E点,AB与O1C相交于M点.
的延长线交于E点,AB与O1C相交于M点. (2007•上海模拟)如图,AB与⊙O1与⊙O2分别相切于点A、B,AB与O1O2相交于点P,已知⊙O1与⊙O2的半径分别为3,6,PA=4,那么AB=
(2007•上海模拟)如图,AB与⊙O1与⊙O2分别相切于点A、B,AB与O1O2相交于点P,已知⊙O1与⊙O2的半径分别为3,6,PA=4,那么AB=
