题目内容
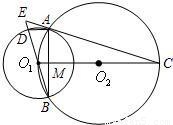
如图,AB是⊙O1与⊙O2的公共弦,O1在⊙O2上,BD,O1C分别是⊙O1与⊙O2的直径,CA与BD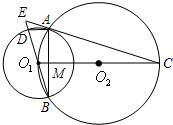 的延长线交于E点,AB与O1C相交于M点.
的延长线交于E点,AB与O1C相交于M点.(1)求证:EA是⊙O1的切线;
(2)连接AD,求证:AD∥O1C;
(3)若DE=1,设⊙O1与⊙O2的半径分别为r,R,且
| r |
| R |
| 1 |
| 2 |
分析:(1)连接O1A,根据圆周角的性质,易得O1A⊥AE;故AE是⊙O1的切线.
(2)根据圆周角定理,可得∠O1BA=∠O1CA;在⊙O1中,根据弦切角定理易得∠DAE=∠O1BA;变化可得AD∥O1C;
(3)根据题意有R=2r;在Rt△AO1C中根据切割线定理可得O1M=
r;再根据平行线的性质;易得
r=
,代入数据即可得到答案.
(2)根据圆周角定理,可得∠O1BA=∠O1CA;在⊙O1中,根据弦切角定理易得∠DAE=∠O1BA;变化可得AD∥O1C;
(3)根据题意有R=2r;在Rt△AO1C中根据切割线定理可得O1M=
| 1 |
| 4 |
| 1 |
| 2 |
| 4r |
| 1+r |
解答: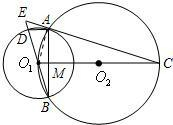 (1)证明:连接O1A,(1分)
(1)证明:连接O1A,(1分)
∵O1C是⊙O2的直径,
∴∠O1AC=90°,(2分)
∴O1A⊥AE.
又∵点A在⊙O1上,
∴AE是⊙O1的切线.(3分)
(2)证明:在⊙O2中,∠O1BA与∠O1CA都是
上的圆周角,
∴∠O1BA=∠O1CA.(4分)
在⊙O1中,由弦切角定理,得∠DAE=∠O1BA,(5分)
∴∠O1CA=∠DAE.(6分)
∴AD∥O1C.(7分)
(3)解:∵
=
,R=2r,
在Rt△AO1C中,O1A2=O1M•O1C,r2=O1M•2R=O1M•4r,
即O1M=
r.(8分)
∵在Rt△BAD中,O1M∥AD,
∴
=
.
即
=
,AD=
r.①
∵在△EO1C中,AD∥O1C,
∴
=
,
=
即AD=
;②(9分)
由①和②得
r=
,解之,得r=7.(10分)
(3)解法二:∵∠DBA=∠O1CA,∠DAB=∠O1AC=90°,
∴△DBA∽△O1CA.
又∵
=
,
∴
=
=
=
.(8分)
设DA=x,
∴O1D=O1A=2x,O1C=8x.
∵DA∥O1C,ED=1,EO1=1+2x,
∴
=
,
=
,(9分)
解之,得x=
.
∴r=2x=7.(10分)
 (1)证明:连接O1A,(1分)
(1)证明:连接O1A,(1分)∵O1C是⊙O2的直径,
∴∠O1AC=90°,(2分)
∴O1A⊥AE.
又∵点A在⊙O1上,
∴AE是⊙O1的切线.(3分)
(2)证明:在⊙O2中,∠O1BA与∠O1CA都是
 |
| O1A |
∴∠O1BA=∠O1CA.(4分)
在⊙O1中,由弦切角定理,得∠DAE=∠O1BA,(5分)
∴∠O1CA=∠DAE.(6分)
∴AD∥O1C.(7分)
(3)解:∵
| r |
| R |
| 1 |
| 2 |
在Rt△AO1C中,O1A2=O1M•O1C,r2=O1M•2R=O1M•4r,
即O1M=
| 1 |
| 4 |
∵在Rt△BAD中,O1M∥AD,
∴
| O1M |
| AD |
| BO1 |
| BD |
即
| ||
| AD |
| r |
| 2r |
| 1 |
| 2 |
∵在△EO1C中,AD∥O1C,
∴
| ED |
| EO1 |
| AD |
| O1C |
| 1 |
| 1+r |
| AD |
| 4r |
即AD=
| 4r |
| 1+r |
由①和②得
| 1 |
| 2 |
| 4r |
| 1+r |
(3)解法二:∵∠DBA=∠O1CA,∠DAB=∠O1AC=90°,
∴△DBA∽△O1CA.
又∵
| r |
| R |
| 1 |
| 2 |
∴
| DA |
| O1A |
| BD |
| O1C |
| 2r |
| 2R |
| 1 |
| 2 |
设DA=x,
∴O1D=O1A=2x,O1C=8x.
∵DA∥O1C,ED=1,EO1=1+2x,
∴
| ED |
| EO1 |
| DA |
| O1C |
| 1 |
| 1+2x |
| x |
| 8x |
解之,得x=
| 7 |
| 2 |
∴r=2x=7.(10分)
点评:本题考查常见的几何题型,包括切线的判定、线线平行的证明及线段长度的求法,要求学生掌握常见的解题方法,并能结合图形选择简单的方法解题.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
 15、已知:如图,AB是⊙O1与⊙O2的公共弦,过B点的直线CD分别交⊙O1于C点,交⊙O2于D点,∠BAD的平分线AM交⊙O1于E点,交直线CD于F点,交⊙O2于M点.
15、已知:如图,AB是⊙O1与⊙O2的公共弦,过B点的直线CD分别交⊙O1于C点,交⊙O2于D点,∠BAD的平分线AM交⊙O1于E点,交直线CD于F点,交⊙O2于M点. O2于D点,∠BAD的平分线AM交⊙O1于E点,交直线CD于F点,交⊙O2于M点.
O2于D点,∠BAD的平分线AM交⊙O1于E点,交直线CD于F点,交⊙O2于M点.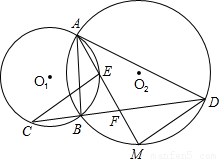
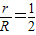 ,求r的长.
,求r的长.