题目内容
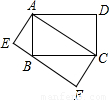
如图:设矩形ABCD的面积是36cm2,在边AB、AD上分别取点E、F,使AE=3EB,DF=2AF,DE与CF的交点为P,则△FPD 的面积是
的面积是分析:延长DE,CB交于点M,构建相似三角形△ADE∽△BME、△FPD∽△CPM,然后根据相似三角形的对应边成比例求得AD=3MB、PC=2PF;作PN⊥AD于点N,构建△DPF的高线和平行线PN∥DC,利用平行线截线段成比例求得3PN=CD,∴PN=
CD,DF=
AD,然后根据三角形的面积公式解答.
| 1 |
| 3 |
| 2 |
| 3 |
解答:解:延长DE,CB交于点M,作PN⊥AD于点N.
在△ADE和△BME中,
,
∴△ADE∽△BME(AA);
又AE=3EB(已知),
∴
=
=
(相似三角形的对应边成比例);
∵DF=2AF,
∴设MB=x,则AD=BC=3x,DF=2x;
在△FPD和△CPM中,
,
∴△FPD∽△CPM,
则
=
=
;
而PN∥CD,
则
=
=
,
∴PN=
CD,DF=
AD,
∴PN•DF=
AD•CD=
×36=8
∴三角形PDF的面积=
DF×PD=
×8=4;
故答案是:4.
在△ADE和△BME中,

|
∴△ADE∽△BME(AA);
又AE=3EB(已知),
∴
| MB |
| AD |
| EB |
| EA |
| 1 |
| 3 |
∵DF=2AF,
∴设MB=x,则AD=BC=3x,DF=2x;
在△FPD和△CPM中,
|
∴△FPD∽△CPM,
则
| PF |
| PC |
| DF |
| MC |
| 1 |
| 2 |
而PN∥CD,
则
| PF |
| FC |
| PN |
| CD |
| 1 |
| 3 |
∴PN=
| 1 |
| 3 |
| 2 |
| 3 |
∴PN•DF=
| 2 |
| 9 |
| 2 |
| 9 |
∴三角形PDF的面积=
| 1 |
| 2 |
| 1 |
| 2 |
故答案是:4.
点评:本题考查了相似三角形的判定与性质、矩形的性质.解答本题的关键是通过作辅助线“延长DE,CB交于点M”构建相似三角形,然后由相似三角形的性质来求所求△PFD的面积与矩形的面积之间的数量关系.

练习册系列答案
相关题目
 如图,设矩形ABCD和矩形AEFC的面积分别为S1、S2,则二者的大小关系是:S1
如图,设矩形ABCD和矩形AEFC的面积分别为S1、S2,则二者的大小关系是:S1
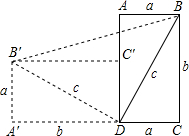
 (a+b)(a+b)=
(a+b)(a+b)=