题目内容
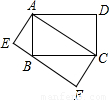
 如图,设矩形ABCD和矩形AEFC的面积分别为S1、S2,则二者的大小关系是:S1
如图,设矩形ABCD和矩形AEFC的面积分别为S1、S2,则二者的大小关系是:S1分析:由于矩形ABCD的面积等于2个△ABC的面积,而△ABC的面积又等于矩形AEFC的一半,所以可得两个矩形的面积关系.
解答:解:矩形ABCD的面积S=2S△ABC,而S△ABC=
S矩形AEFC,即S1=S2,故此题答案为=.
| 1 |
| 2 |
点评:本题主要考查了矩形的性质及面积的计算,能够熟练运用矩形的性质进行一些面积的计算问题.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
 的面积是
的面积是
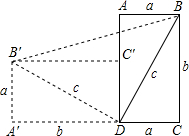
 (a+b)(a+b)=
(a+b)(a+b)=