题目内容
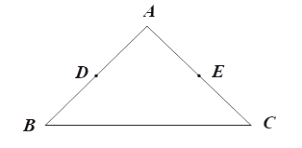
【题目】在△ABC中,![]() ,
,![]() 分别是
分别是![]() 两边的中点,如果
两边的中点,如果![]() 上的所有点都在△ABC的内部或边上,则称
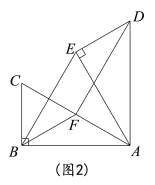
上的所有点都在△ABC的内部或边上,则称![]() 为△ABC的中内弧.例如,下图中
为△ABC的中内弧.例如,下图中![]() 是△ABC的一条中内弧.
是△ABC的一条中内弧.

(1)如图,在Rt△ABC中,![]() 分别是
分别是![]() 的中点.画出△ABC的最长的中内弧
的中点.画出△ABC的最长的中内弧![]() ,并直接写出此时
,并直接写出此时![]() 的长;
的长;
(2)在平面直角坐标系中,已知点![]() ,在△ABC中,
,在△ABC中,![]() 分别是
分别是![]() 的中点.
的中点.
①若![]() ,求△ABC的中内弧
,求△ABC的中内弧![]() 所在圆的圆心
所在圆的圆心![]() 的纵坐标的取值范围;
的纵坐标的取值范围;
②若在△ABC中存在一条中内弧![]() ,使得
,使得![]() 所在圆的圆心P在△ABC的内部或边上,直接写出t的取值范围.
所在圆的圆心P在△ABC的内部或边上,直接写出t的取值范围.
【答案】(1)![]() ;(2)①P的纵坐标
;(2)①P的纵坐标![]() 或
或![]() ;②
;②![]() .
.
【解析】
(1)由三角函数值及等腰直角三角形性质可求得DE=2,最长中内弧即以DE为直径的半圆,![]() 的长即以DE为直径的圆周长的一半;
的长即以DE为直径的圆周长的一半;
(2)根据三角形中内弧定义可知,圆心一定在DE的中垂线上,,①当![]() 时,要注意圆心P在DE上方的中垂线上均符合要求,在DE下方时必须AC与半径PE的夹角∠AEP满足90°≤∠AEP<135°;②根据题意,t的最大值即圆心P在AC上时求得的t值.
时,要注意圆心P在DE上方的中垂线上均符合要求,在DE下方时必须AC与半径PE的夹角∠AEP满足90°≤∠AEP<135°;②根据题意,t的最大值即圆心P在AC上时求得的t值.
解:(1)如图2,
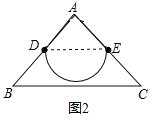
以DE为直径的半圆弧![]() ,就是△ABC的最长的中内弧
,就是△ABC的最长的中内弧![]() ,连接DE,∵∠A=90°,AB=AC=2
,连接DE,∵∠A=90°,AB=AC=2![]() ,D,E分别是AB,AC的中点,
,D,E分别是AB,AC的中点,![]() ,
,
∴弧![]()
![]() ;
;
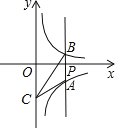
(2)如图3,由垂径定理可知,圆心一定在线段DE的垂直平分线上,连接DE,作DE垂直平分线FP,作EG⊥AC交FP于G,

①当![]() 时,C(2,0),∴D(0,1),E(1,1),
时,C(2,0),∴D(0,1),E(1,1),![]() ,
,
设![]() 由三角形中内弧定义可知,圆心线段DE上方射线FP上均可,∴m≥1,
由三角形中内弧定义可知,圆心线段DE上方射线FP上均可,∴m≥1,
∵OA=OC,∠AOC=90°
∴∠ACO=45°,
∵DE∥OC
∴∠AED=∠ACO=45°
作EG⊥AC交直线FP于G,FG=EF=![]()
根据三角形中内弧的定义可知,圆心在点G的下方(含点G)直线FP上时也符合要求;
![]()
综上所述,![]() 或m≥1.
或m≥1.
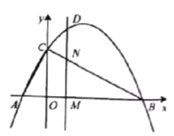
②图4,设圆心P在AC上,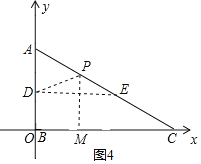
∵P在DE中垂线上,
∴P为AE中点,作PM⊥OC于M,则PM=![]()
![]() ,
,
∵DE∥BC
∴∠ADE=∠AOB=90°,
![]()
∵PD=PE,
∴∠AED=∠PDE
∵∠AED+∠DAE=∠PDE+∠ADP=90°,
∴∠DAE=∠ADP
![]()
由三角形中内弧定义知,PD≤PM
![]() ,AE≤3,即
,AE≤3,即![]() ,解得:
,解得:![]()


【题目】小云想用7天的时间背诵若干首诗词,背诵计划如下:
①将诗词分成4组,第i组有![]() 首,i =1,2,3,4;
首,i =1,2,3,4;
②对于第i组诗词,第i天背诵第一遍,第(![]() )天背诵第二遍,第(
)天背诵第二遍,第(![]() )天背诵第三遍,三遍后完成背诵,其它天无需背诵,
)天背诵第三遍,三遍后完成背诵,其它天无需背诵,![]() 1,2,3,4;
1,2,3,4;
第1天 | 第2天 | 第3天 | 第4天 | 第5天 | 第6天 | 第7天 | |
第1组 |
|
|
| ||||
第2组 |
|
|
| ||||
第3组 | |||||||
第4组 |
|
|
|
③每天最多背诵14首,最少背诵4首.
解答下列问题:
(1)填入![]() 补全上表;
补全上表;
(2)若![]() ,
,![]() ,
,![]() ,则
,则![]() 的所有可能取值为______;
的所有可能取值为______;
(3)7天后,小云背诵的诗词最多为______首.