ƒøƒ⁄»ð
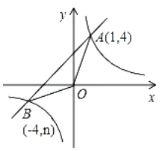
°æƒø°ø»ÁÕº£¨Rt°˜OAB»ÁÕºÀ˘ æ∑≈÷√‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨÷±Ω«±þOA”Îx÷·÷ÿ∫œ£¨°œOAB=90°„£¨OA=4£¨AB=2£¨∞—Rt°˜OAB»∆µ„OƒÊ ±’Ζ˝◊™90°„£¨µ„B–˝◊™µΩµ„CµƒŒª÷√£¨≈◊ŒÔœþy=ax2+bxæ≠π˝µ„C°¢A.

£®1£©«Û∏√≈◊ŒÔœþµƒΩ‚Œˆ Ω£ª
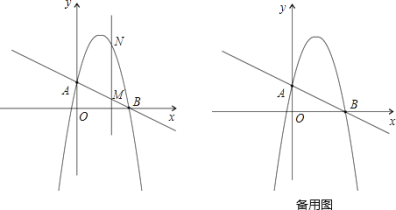
£®2£©‘⁄x÷·…œ∑Ωµƒ≈◊ŒÔœþ…œ”–“ª∂ص„P£¨π˝µ„P◊˜x÷·µƒ∆Ω––œþΩª≈◊ŒÔœþ”⁄µ„M£¨∑÷±π˝µ„P£¨µ„M◊˜x÷·µƒ¥πœþ£¨Ωªx÷·”⁄R°¢S¡Ωµ„£¨Œ £∫Àƒ±þ–ŒPRSMµƒ÷Ð≥§ «∑Ò”–◊Ó¥Û÷µ£ø»Áπ˚”–£¨«Î«Û≥ˆ◊Ó÷µ£¨≤¢–¥≥ˆΩ‚¥π˝≥㪻Áπ˚√ª”–£¨«ÎÀµ√˜¿Ì”…£Æ
£®3£©‘⁄x÷·…œ∑Ωµƒ≈◊ŒÔœþ…œ «∑ҥʑ⁄µ„Q,π˝µ„Q◊˜x÷·µƒ¥πœþ£¨¥π◊„Œ™H, πµ√“‘O°¢Q°¢HŒ™∂•µ„µƒ»˝Ω«–Œ”ÎOABœýÀ∆£¨»Áπ˚¥Ê‘⁄£¨÷±Ω”–¥≥ˆµ„Qµƒ◊¯±Í£¨»Áπ˚≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…°£
°æ¥∞∏°ø£®1£©![]() £ª£®2£©”–£¨◊Ó¥Û÷µŒ™10£¨π˝≥ì‘£ª£®3£©¥Ê‘⁄£¨Q1(2,4)£ªQ2 (
£ª£®2£©”–£¨◊Ó¥Û÷µŒ™10£¨π˝≥ì‘£ª£®3£©¥Ê‘⁄£¨Q1(2,4)£ªQ2 (![]() ).
).
°æΩ‚Œˆ°ø
£®1£©∏˘æð–˝◊™µƒ–‘÷ ø…«Û≥ˆCµƒ◊¯±Í∫ÕAµƒ◊¯±Í£¨”÷“ÚŒ™≈◊ŒÔœþæ≠π˝‘≠µ„£¨π …Ëy=ax2+bx∞—£®2£¨4£©£¨£®4£¨0£©¥˙»Î£¨«Û≥ˆa∫Õbµƒ÷µº¥ø…«Û≥ˆ∏√≈◊ŒÔœþµƒΩ‚Œˆ Ω£ª
£®2£©Àƒ±þ–ŒPRSMµƒ÷Ð≥§”–◊Ó¥Û÷µ£¨…˵„Pµƒ◊¯±ÍŒ™P£®a£¨-a2+4a£©‘Ú”…≈◊ŒÔœþµƒ∂‘≥∆–‘÷™OR=AS£¨À˘“‘RS=PM=4-2a£¨PR=MS=-a2+4a£¨‘Úæÿ–ŒPRSMµƒ÷Ð≥§L=2[4-2a+£®-a2+4a£©]=-2£®a-1£©2+10£¨¿˚”√∫Ø ˝µƒ–‘÷ º¥ø…«Û≥ˆÀƒ±þ–ŒPRSMµƒ÷Ð≥§µƒ◊Ó¥Û÷µ£Æ
£®3£©∑÷±º∆À„°˜OHQ°◊°˜BAO∫Õ°˜OHQ°◊°˜OAB ±Qµ„µƒ◊¯±Í£¨∑÷Œˆ∫Ûº¥ø…Ω‚¥.
Ω‚£∫£®1£©°þOA=4£¨AB=2£¨°˜AOB»∆µ„OƒÊ ±’Ζ˝◊™90°„£¨µ„B–˝◊™µΩµ„CµƒŒª÷√£¨°ýµ„Cµƒ◊¯±ÍŒ™£®2£¨4£©£Æ
”÷°þµ„Aµƒ◊¯±ÍŒ™£®4£¨0£©£¨≈◊ŒÔœþæ≠π˝‘≠µ„£¨π …Ëy=ax2+bx£®a°Ÿ0£©£¨∞—£®2£¨4£©£¨£®4£¨0£©¥˙»Î£¨µ√![]() £¨
£¨
Ω‚µ√![]() £¨À˘“‘≈◊ŒÔœþµƒΩ‚Œˆ ΩŒ™y=-x2+4x£ª
£¨À˘“‘≈◊ŒÔœþµƒΩ‚Œˆ ΩŒ™y=-x2+4x£ª
£®2£©”–◊Ó¥Û÷µ£Æ»ÁÕº£¨
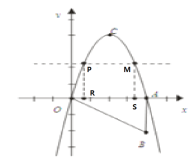
¿Ì”…»Áœ¬£∫…˵„Pµƒ◊¯±ÍŒ™P£®a£¨-a2+4a£©£¨PR=MS=-a2+4a£¨
‘Ú”…≈◊ŒÔœþµƒ∂‘≥∆–‘÷™OR=AS£¨À˘“‘RS=PM=4-2a£¨
‘Úæÿ–ŒPRSMµƒ÷Ð≥§L=2[4-2a+£®-a2+4a£©]=-2£®a-1£©2+10£¨
À˘“‘µ±a=1 ±£¨æÿ–ŒPRSMµƒ÷Ð≥§”–◊Ó¥Û÷µ£¨Lmax=10£Æ
£®3£©…ËHµ„◊¯±ÍŒ™£®n£¨0£©,‘ÚOH=n£¨QH=-n+4n£¨
¢ŸºŸ…Ë°˜OHQ°◊°˜BAO£¨‘Ú![]() ,
,
ø…µ√![]() £¨Ω‚µ√
£¨Ω‚µ√![]() =2£¨
=2£¨![]() =0£®…·»•£©£¨
=0£®…·»•£©£¨
¥˙»Îø…µ√Qµ„◊¯±ÍŒ™£®2£¨4£©£ª
¢⁄ºŸ…Ë°˜OHQ°◊°˜OAB£¨‘Ú![]() ,
,
![]() £¨Ω‚µ√
£¨Ω‚µ√![]() =
=![]() £¨
£¨![]() =0£®…·»•£©£¨
=0£®…·»•£©£¨
¥˙»Îø…µ√Qµ„◊¯±ÍŒ™£®![]() £¨
£¨![]() £©£ª
£©£ª
◊€…œÀ˘ ˆQµ„◊¯±ÍŒ™£®2£¨4£©ªÚ£®![]() £¨
£¨![]() £©.
£©.

°æƒø°ø£®…˙ªÓπ€≤Ï£©º◊°¢““¡Ω»À¬Ú≤À£¨º◊œ∞πþ¬Ú“ª∂®÷ ¡øµƒ≤À£¨““œ∞πþ¬Ú“ª∂®Ω∂Óµƒ≤À£¨¡Ω»À√ø¥Œ¬Ú≤Àµƒµ•º€œýÕ¨£¨¿˝»Á£∫
≤Àº€ | ||
÷ ¡ø | Ω∂Ó | |
º◊ |
|
|
““ |
|
|
≤Àº€ | ||
÷ ¡ø | Ω∂Ó | |
º◊ |
| ____‘™ |
““ | ____«ßøÀ |
|
£®1£©ÕÍ≥……œ±Ì£ª
£®2£©º∆À„º◊¡Ω¥Œ¬Ú≤Àµƒæ˘º€∫Õ““¡Ω¥Œ¬Ú≤Àµƒæ˘º€£Æ£®æ˘º€![]() ◊ÐΩ∂Ó◊Ð÷ ¡ø£©
◊ÐΩ∂Ó◊Ð÷ ¡ø£©
£® ˝—ßÀºøº£©…˺◊√ø¥Œ¬Ú÷ ¡øŒ™![]() «ßøÀµƒ≤À£¨““√ø¥Œ¬ÚΩ∂ÓŒ™
«ßøÀµƒ≤À£¨““√ø¥Œ¬ÚΩ∂ÓŒ™![]() ‘™µƒ≤À£¨¡Ω¥Œµƒµ•º€∑÷± «
‘™µƒ≤À£¨¡Ω¥Œµƒµ•º€∑÷± «![]() ‘™
‘™![]() «ßøÀ°¢
«ßøÀ°¢![]() ‘™
‘™![]() «ßøÀ£¨”√∫¨”–
«ßøÀ£¨”√∫¨”–![]() °¢
°¢![]() °¢
°¢![]() °¢
°¢![]() µƒ Ω◊”£¨∑÷±±Ì æ≥ˆº◊°¢““¡Ω¥Œ¬Ú≤Àµƒæ˘º€
µƒ Ω◊”£¨∑÷±±Ì æ≥ˆº◊°¢““¡Ω¥Œ¬Ú≤Àµƒæ˘º€![]() °¢
°¢![]() £Æ±»Ωœ
£Æ±»Ωœ![]() °¢
°¢![]() µƒ¥Û–°£¨≤¢Àµ√˜¿Ì”…£Æ
µƒ¥Û–°£¨≤¢Àµ√˜¿Ì”…£Æ
£®÷™ ∂«®“∆£©ƒ≥¥¨‘⁄œýæýŒ™![]() µƒº◊°¢““¡Ω¬ÎÕ∑º‰Õ˘∑µ∫Ω––“ª¥Œ£¨‘⁄√ª”–ÀÆ¡˜ ±£¨¥¨µƒÀŸ∂»Œ™
µƒº◊°¢““¡Ω¬ÎÕ∑º‰Õ˘∑µ∫Ω––“ª¥Œ£¨‘⁄√ª”–ÀÆ¡˜ ±£¨¥¨µƒÀŸ∂»Œ™![]() À˘–Ë ±º‰Œ™£∫»Áπ˚ÀÆ¡˜ÀŸ∂»Œ™
À˘–Ë ±º‰Œ™£∫»Áπ˚ÀÆ¡˜ÀŸ∂»Œ™![]() ±£®
±£®![]() £©£¨¥¨À≥ÀÆ∫Ω––ÀŸ∂»Œ™£®
£©£¨¥¨À≥ÀÆ∫Ω––ÀŸ∂»Œ™£®![]() £©£¨ƒÊÀÆ∫Ω––ÀŸ∂»Œ™£®
£©£¨ƒÊÀÆ∫Ω––ÀŸ∂»Œ™£®![]() £©£¨À˘–Ë ±º‰Œ™
£©£¨À˘–Ë ±º‰Œ™![]() «ÎΩ˺¯…œ√ʵƒ—–æøæ≠—È£¨±»Ωœ
«ÎΩ˺¯…œ√ʵƒ—–æøæ≠—È£¨±»Ωœ![]() °¢
°¢![]() µƒ¥Û–°£¨≤¢Àµ√˜¿Ì”…£Æ
µƒ¥Û–°£¨≤¢Àµ√˜¿Ì”…£Æ