Question

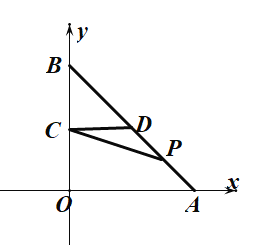
【题目】如图，在平面直角坐标系内，点为坐标原点，轴上点的横坐标为，轴上点的纵坐标为，且，过中点作轴的平行线交于点

（1）求点的坐标；

（2）第一象限的点在上，点的横坐标为，的面积为（），用含的式子表示，并直接写出相应的的范围；

（3）在（2）的条件下，过点作直线的垂线，点为垂足，的平分线交于点，交轴正半轴于点，若，求值．

Answer 1

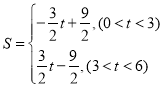【答案】（1）；（2）；（3）

【解析】

（1）先对原式进行整理，根据二次根式与平方的非负性求出a,b的值，再利用三角形中位线的性质即可求出D的横纵坐标；

（2）先用待定系数法求出直线AB的解析式，然后分两种情况：P点在直线CD的上方和下方，利用三角形的面积公式即可表示出S与t之间的关系式；

（3）过点作的垂线，点为垂足，的延长线交的延长线于点，过点作的垂线，点T为垂足，先证明得出，然后利用角平分线的性质和等腰直角三角形的性质证明，则有 ，，进而得出，接着证明得出 ， ，进而有，最后分别用含t的代数式表示出和，求出t的值，则可求．

（1）解：∵

即

∴

∴

∵CD是的中位线

∴

∴

（2）设直线AB的解析式为

将点代入解析式中得

解得

∴直线AB的解析式为

当时，

设底边CD上的高为h，

当时，

∴（）

当时，

∴（）

综上所述，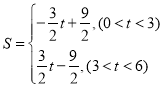

（3）过点作的垂线，点为垂足，的延长线交的延长线于点，过点作的垂线，点T为垂足．

∵

∴

在和中，

平分

即

∴

∵

在和中，

∴

∴

∴

∵

∴

在和中，

∴

∴

∴

解得

∴