题目内容
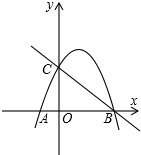 如图所示,直线y=-x+3与x轴、y轴分别交于点B、C,抛物线y=-x2+bx+c 经过点B、C,点A是抛物线与x轴的另一个交点.
如图所示,直线y=-x+3与x轴、y轴分别交于点B、C,抛物线y=-x2+bx+c 经过点B、C,点A是抛物线与x轴的另一个交点.(1)求抛物线的解析式;
(2)求△ABC的面积;
(3)若P是抛物线上一点,且S△ABP=
| 1 |
| 2 |
考点:待定系数法求二次函数解析式,抛物线与x轴的交点
专题:
分析:(1)先根据直线y=-x+3求出B、C两点的坐标,然后将它们代入抛物线中即可求出待定系数的值.
(2)令y=0,则-x2+2x+3=0,解方程即可求得;
(3)根据已知求得P的纵坐标,代入y=-x2+2x+3即可求得P的坐标.
(2)令y=0,则-x2+2x+3=0,解方程即可求得;
(3)根据已知求得P的纵坐标,代入y=-x2+2x+3即可求得P的坐标.
解答:解:(1)直线y=-x+3与坐标轴的两个交点坐标分别是
B(3,0),C(0,3),
∵抛物线y=-x2+bx+c经过B、C两点,
∴c=3
∴-9+3b+3=0,
得到b=2,
∴抛物线的解析式.
(2)令y=0,则-x2+2x+3=0,
解得x1=-1,x2=3,
∴A的坐标为(-1,0),
∴AB=4,
∴S△ABC=
AB•yc=
×4×3=6;
(3)设P的纵坐标为n,
∵S△ABP=
S△ABC,
∴S△ABP=3,
即
AB•|n|=3,解得n=±
,
∴±
=-x2+2x+3,解x=
或x=
,
∴这样的点P有4个,它们分别是(
,
),(
,
),(
,-
),(
,-
).
B(3,0),C(0,3),
∵抛物线y=-x2+bx+c经过B、C两点,
∴c=3
∴-9+3b+3=0,
得到b=2,
∴抛物线的解析式.
(2)令y=0,则-x2+2x+3=0,
解得x1=-1,x2=3,
∴A的坐标为(-1,0),
∴AB=4,
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
(3)设P的纵坐标为n,
∵S△ABP=
| 1 |
| 2 |
∴S△ABP=3,
即
| 1 |
| 2 |
| 3 |
| 2 |
∴±
| 3 |
| 2 |
2±
| ||
| 2 |
2±
| ||
| 2 |
∴这样的点P有4个,它们分别是(
2+
| ||
| 2 |
| 3 |
| 2 |
2-
| ||
| 2 |
| 3 |
| 2 |
2+
| ||
| 2 |
| 3 |
| 2 |
2-
| ||
| 2 |
| 3 |
| 2 |
点评:本题主要考查了二次函数解析式的确定、函数图象交点的求法、图形面积的求法等知识点.考查了学生数形结合的数学思想方法.

练习册系列答案
相关题目
下面的语句正确的是( )
| A、一个角小于它的补角 |
| B、一个角只有一个补角 |
| C、一个锐角不等于它的余角 |
| D、一个角的补角等于这个角与它余角的两倍的和 |
若分式
的值为负,则x的取值范围是( )
| 3 |
| 2x+1 |
A、x>-
| ||
B、x<-
| ||
C、x≥-
| ||
D、x≤-
|
设[x)表示大于x的最小整数,如[3)=4,[-1.2)=-1,则下列结论中正确的有( )
①[0)=0;②[x)-x的最小值是0;③[x)-x的最大值是0;④存在实数x,使[x)-x=0.5成立.
①[0)=0;②[x)-x的最小值是0;③[x)-x的最大值是0;④存在实数x,使[x)-x=0.5成立.
| A、1个 | B、2个 | C、3个 | D、4个 |
 a、b在数轴如图表示,则|a|+|b|-|a-b|=( )
a、b在数轴如图表示,则|a|+|b|-|a-b|=( )| A、2a | B、2b |
| C、0 | D、2a-2b |