题目内容
1.求l+2+22+23+…+220l3的值,可令:S=l+2+22+23+…+220l3,则 2S=2+22+23+…+22014,因此2S-S=220l4-1.仿照以上推理,计算出1+3+32+33+…+320l6=$\frac{{3}^{2017}-1}{2}$.分析 仿照例子,令S=1+3+32+33+…+32016,则可得出3S=3+32+33+…+32016+32017,两者做差后除以2即可得出结论.
解答 解:令S=1+3+32+33+…+32016,则3S=3+32+33+…+32016+32017,
∴S=$\frac{3S-S}{2}$=$\frac{{3}^{2017}-1}{2}$.
故答案为:$\frac{{3}^{2017-1}}{2}$.
点评 本题考查了规律型中的数字的变化类,解题的关键是仿照例子计算1+3+32+33+…+32016,本题其实是等比数列的求和公式,但初中未接触过该方面的知识,需要借助于错位相减法来求出结论.

练习册系列答案
相关题目
12.下列图形中,∠1和∠2互为余角的是( )
| A. |  | B. |  | C. |  | D. |  |
16.方程x2+3x-6=0与x2-6x+3=0所有根的乘积等于( )
| A. | -18 | B. | -3 | C. | 3 | D. | 18 |
5.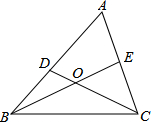 如图,∠A,∠DOE,∠BEC的大小关系是( )
如图,∠A,∠DOE,∠BEC的大小关系是( )
 如图,∠A,∠DOE,∠BEC的大小关系是( )
如图,∠A,∠DOE,∠BEC的大小关系是( )| A. | ∠A>∠DOE>∠BEC | B. | ∠DOE>∠BEC>∠A | C. | ∠DOE>∠A>∠BEC | D. | ∠BEC>∠DOE>∠A |
 如图,已知AC是矩形ABCD的对角线,过AC的中点O的直线EF,交BC于点F,交BC于点F,交AD于点E,连接AF,CE.
如图,已知AC是矩形ABCD的对角线,过AC的中点O的直线EF,交BC于点F,交BC于点F,交AD于点E,连接AF,CE. 已知图中的每个小正方格都是边长为1的小正方形,若△ABC与△A1B1C1是位似图形,且顶点都在小正方形顶点上,则它们的位似中心的坐标是(9,0).
已知图中的每个小正方格都是边长为1的小正方形,若△ABC与△A1B1C1是位似图形,且顶点都在小正方形顶点上,则它们的位似中心的坐标是(9,0). 如图所示五角星,试求∠A+∠B+∠C+∠D+∠E.
如图所示五角星,试求∠A+∠B+∠C+∠D+∠E.