题目内容
 如图,AP是∠MAN的平分线,B是射线AN上的一点,以AB为直径作⊙O交AP于点C,过点C作CD⊥AM于点D.
如图,AP是∠MAN的平分线,B是射线AN上的一点,以AB为直径作⊙O交AP于点C,过点C作CD⊥AM于点D.(1)判断直线DC与⊙O的位置关系,并说明理由;
(2)若OA=6,AD=10,求CD的长.
考点:切线的判定,全等三角形的判定与性质
专题:
分析:(1)连接OC,由OA=OC得∠OAC=∠OCA,由AP平分∠MAN得∠DAC=∠CAO,则∠DAC=∠OCA,根据平行线的判定得到AD∥OC,而AD⊥CD,所以OC⊥CD,然后根据切线的判定定理得到直线DC与⊙O相切;
(2)作CE⊥AB于E,先根据角平分线性质得CD=CE,在根据“HL”判断Rt△ADC≌Rt△AEC,得到AE=AD=10,则OE=4,在Rt△OCE中根据勾股定理计算出CE即可.
(2)作CE⊥AB于E,先根据角平分线性质得CD=CE,在根据“HL”判断Rt△ADC≌Rt△AEC,得到AE=AD=10,则OE=4,在Rt△OCE中根据勾股定理计算出CE即可.
解答:解: (1)直线DC与⊙O相切.理由如下:
(1)直线DC与⊙O相切.理由如下:
连接OC,如图,
∵OA=OC,
∴∠OAC=∠OCA,
∵AP平分∠MAN,
∴∠DAC=∠CAO,
∴∠DAC=∠OCA,
∴AD∥OC,
又∵AD⊥CD,
∴OC⊥CD,且O点为⊙O半径,
∴直线DC与⊙O相切;
(2)作CE⊥AB于E,如图,
∵AP平分∠MAN,CD⊥AM,
∴CD=CE,
在Rt△ADC和Rt△AEC中
,
∴Rt△ADC≌Rt△AEC(HL),
∴AE=AD=10,
∴OE=AE-OA=4,
在Rt△OCE中,OC=6,OE=4,
∴CE=
=2
,
∴CD=2
.
 (1)直线DC与⊙O相切.理由如下:
(1)直线DC与⊙O相切.理由如下:连接OC,如图,
∵OA=OC,
∴∠OAC=∠OCA,
∵AP平分∠MAN,
∴∠DAC=∠CAO,
∴∠DAC=∠OCA,
∴AD∥OC,
又∵AD⊥CD,
∴OC⊥CD,且O点为⊙O半径,
∴直线DC与⊙O相切;
(2)作CE⊥AB于E,如图,
∵AP平分∠MAN,CD⊥AM,
∴CD=CE,
在Rt△ADC和Rt△AEC中
|
∴Rt△ADC≌Rt△AEC(HL),
∴AE=AD=10,
∴OE=AE-OA=4,
在Rt△OCE中,OC=6,OE=4,
∴CE=
| OC2-OE2 |
| 5 |
∴CD=2
| 5 |
点评:本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.也考查了勾股定理和角平分线性质.

练习册系列答案
相关题目
在实数
、0、π、3.1415、-3、
、2.10100110001…中,无理数的个数为( )
| 5 |
| 4 |
| A、2个 | B、3个 | C、4个 | D、5个 |
下面在平面直角坐标系中所给的四个图象中,是函数图象的是( )
A、 |
B、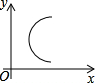 |
C、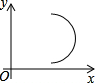 |
D、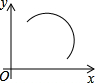 |
 如图,已知∠AOB=30°,点P为∠AOB内一点,OP=10cm,分别作出P点关于OA、OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,则△PMN的周长为
如图,已知∠AOB=30°,点P为∠AOB内一点,OP=10cm,分别作出P点关于OA、OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,则△PMN的周长为 如图,某校一幢教学大楼的顶部竖有一块中考倒计时牌CD.小明在山坡的坡脚A处测得倒计时牌底部D的仰角为60°,沿山坡向上走到B处测得倒计时牌顶部C的仰角为45°.已知山坡AB的坡度i=1:
如图,某校一幢教学大楼的顶部竖有一块中考倒计时牌CD.小明在山坡的坡脚A处测得倒计时牌底部D的仰角为60°,沿山坡向上走到B处测得倒计时牌顶部C的仰角为45°.已知山坡AB的坡度i=1: 已知AB=AD,∠BAD=∠CAE,请添加一个条件
已知AB=AD,∠BAD=∠CAE,请添加一个条件 如图,弦CD=EF,请至少找出图中5对具有相等关系的量.
如图,弦CD=EF,请至少找出图中5对具有相等关系的量.