题目内容
18.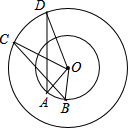 如图,点A,B和点C,D分别在两个同心圆上,且∠AOB=∠COD.求证:∠C=∠D.
如图,点A,B和点C,D分别在两个同心圆上,且∠AOB=∠COD.求证:∠C=∠D.
分析 证得∠BOC=∠AOD,然后运用“SAS”证明△COB≌DOA,即可证得∠C=∠D.
解答 解:∵∠AOB=∠COD,
∴∠AOB+∠AOC=∠COD+∠AOC,即∠BOC=∠AOD,
证明:在△COB和△DOA中
$\left\{\begin{array}{l}{OA=OB}\\{∠BOC=∠AOD}\\{OC=OD}\end{array}\right.$,
∴△COB≌DOA,
∴∠C=∠D.
点评 本题考查了全等三角形的判定与性质、同圆半径相等的性质,熟悉全等三角形的判定方法和圆的有关性质是解决问题的关键.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案
相关题目
6.晚上,站在路灯下的晶晶向远离路灯的方向走去,她发现自己的身影( )
| A. | 变长 | B. | 变短 | C. | 先变长后变短 | D. | 先变短后变长 |
13.放学以后,小明和小华从学校分开,分别向北和东走回家,若小明和小华行走的速度都是50米/分,小明用10分到家,小华用24分到家,小明和小华家的距离为( )
| A. | 600米 | B. | 800米 | C. | 1000米 | D. | 1300米 |
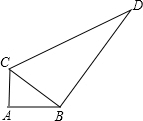 一块试验田的形状如图所示,∠A=90°,AC=3m,AB=4m,BD=12m,CD=13m,求这块试验田的面积.
一块试验田的形状如图所示,∠A=90°,AC=3m,AB=4m,BD=12m,CD=13m,求这块试验田的面积. 如图,AB是⊙O的直径,点P是BA延长线上一点,直线PE切⊙O于点Q,延长PB至C,使BC=PA=2,PQ=4.
如图,AB是⊙O的直径,点P是BA延长线上一点,直线PE切⊙O于点Q,延长PB至C,使BC=PA=2,PQ=4.